Christofides algorithm

The Christofides algorithm or Christofides–Serdyukov algorithm is an algorithm for finding approximate solutions to the travelling salesman problem, on instances where the distances form a metric space (they are symmetric and obey the triangle inequality). It is an approximation algorithm that guarantees that its solutions will be within a factor of 3/2 of the optimal solution length, and is named after Nicos Christofides and Anatoliy I. Serdyukov (Russian: Анатолий Иванович Сердюков); the latter discovered it independently in 1976 (but the publication is dated 1978).

Algorithm

Let G = (V,w) be an instance of the travelling salesman problem. That is, G is a complete graph on the set V of vertices, and the function w assigns a nonnegative real weight to every edge of G. According to the triangle inequality, for every three vertices u, v, and x, it should be the case that w(uv) + w(vx) ≥ w(ux).

Then the algorithm can be described in pseudocode as follows.

1. Create a minimum spanning tree T of G.
2. Let O be the set of vertices with odd degree in T. By the handshaking lemma, O has an even number of vertices.
3. Find a minimum-weight perfect matching M in the subgraph induced in G by O.
4. Combine the edges of M and T to form a connected multigraph H in which each vertex has even degree.
5. Form an Eulerian circuit in H.
6. Make the circuit found in previous step into a Hamiltonian circuit by skipping repeated vertices (shortcutting).

Steps 5 and 6 do not necessarily yield only a single result; as such, the heuristic can give several different paths.

Computational complexity

The worst-case complexity of the algorithm is dominated by the perfect matching step, which has $O(n^{3})$ complexity. Serdyukov's paper claimed $O(n^{3}\log n)$ complexity, because the author was only aware of a less efficient perfect matching algorithm.

Approximation ratio

The cost of the solution produced by the algorithm is within 3/2 of the optimum. To prove this, let C be the optimal traveling salesman tour. Removing an edge from C produces a spanning tree, which must have weight at least that of the minimum spanning tree, implying that w(T) ≤ w(C). Next, number the vertices of O in cyclic order around C, and partition C into two sets of paths: the ones in which the first path vertex in cyclic order has an odd number and the ones in which the first path vertex has an even number. Each set of paths corresponds to a perfect matching of O that matches the two endpoints of each path, and the weight of this matching is at most equal to the weight of the paths. Since these two sets of paths partition the edges of C, one of the two sets has at most half of the weight of C, and thanks to the triangle inequality its corresponding matching has weight that is also at most half the weight of C. The minimum-weight perfect matching can have no larger weight, so w(M) ≤ w(C)/2. Adding the weights of T and M gives the weight of the Euler tour, at most 3w(C)/2. Thanks to the triangle inequality, shortcutting does not increase the weight, so the weight of the output is also at most 3w(C)/2.

Lower bounds

There exist inputs to the travelling salesman problem that cause the Christofides algorithm to find a solution whose approximation ratio is arbitrarily close to 3/2. One such class of inputs are formed by a path of n vertices, with the path edges having weight 1, together with a set of edges connecting vertices two steps apart in the path with weight 1 + ε for a number ε chosen close to zero but positive. All remaining edges of the complete graph have distances given by the shortest paths in this subgraph. Then the minimum spanning tree will be given by the path, of length n − 1, and the only two odd vertices will be the path endpoints, whose perfect matching consists of a single edge with weight approximately n/2. The union of the tree and the matching is a cycle, with no possible shortcuts, and with weight approximately 3n/2. However, the optimal solution uses the edges of weight 1 + ε together with two weight-1 edges incident to the endpoints of the path, and has total weight (1 + ε)(n − 2) + 2, close to n for small values of ε. Hence we obtain an approximation ratio of 3/2.

Example

	Given: complete graph whose edge weights obey the triangle inequality
	Calculate minimum spanning tree T
	Calculate the set of vertices O with odd degree in T
	Form the subgraph of G using only the vertices of O
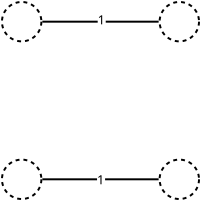	Construct a minimum-weight perfect matching M in this subgraph
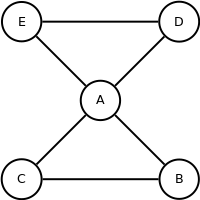	Unite matching and spanning tree T ∪ M to form an Eulerian multigraph
	Calculate Euler tour Here the tour goes A->B->C->A->D->E->A. Equally valid is A->B->C->A->E->D->A.
	Remove repeated vertices, giving the algorithm's output. If the alternate tour would have been used, the shortcut would be going from C to E which results in a shorter route (A->B->C->E->D->A) if this is an euclidean graph as the route A->B->C->D->E->A has intersecting lines which is proven not to be the shortest route.

Further developments

This algorithm still stands as the best polynomial time approximation algorithm for the stated problem that has been thoroughly peer-reviewed by the relevant scientific community for the traveling salesman problem on general metric spaces. In July 2020 Karlin, Klein, and Gharan released a preprint in which they introduced a novel approximation algorithm and claimed that its approximation ratio is 1.5 − 10⁻³⁶. Theirs is a randomized algorithm and it follows similar principles to Christofides' algorithm, but uses a randomly chosen tree from a carefully chosen random distribution in place of the minimum spanning tree. The paper was published at STOC'21 where it received a best paper award.

In the special case of Euclidean space, for any c > 0, where d is the number of dimensions in the Euclidean space, there is a polynomial-time algorithm that finds a tour of length at most (1 + 1/c) times the optimal for geometric instances of TSP in

$O\left(n(\log n)^{(O(c{\sqrt {d}}))^{d-1}}\right)$ time;

this is called a polynomial-time approximation scheme (PTAS). Sanjeev Arora and Joseph S. B. Mitchell were awarded the Gödel Prize in 2010 for their concurrent discovery of a PTAS for the Euclidean TSP.

External links

• NIST Christofides Algorithm Definition