List of Mersenne primes and perfect numbers

Mersenne primes and perfect numbers are two deeply interlinked types of natural numbers in number theory. Mersenne primes, named after the friar Marin Mersenne, are prime numbers that can be expressed as 2p − 1 for some positive integer p. For example, 3 is a Mersenne prime as it is a prime number and is expressible as 22 − 1.[1][2] The exponents p corresponding to Mersenne primes must themselves be prime, although the vast majority of primes p do not lead to Mersenne primes—for example, 211 − 1 = 2047 = 23 × 89.[3]
Perfect numbers are natural numbers that equal the sum of their positive proper divisors, which are divisors excluding the number itself. So, 6 is a perfect number because the proper divisors of 6 are 1, 2, and 3, and 1 + 2 + 3 = 6.[2][4]
Euclid proved c. 300 BCE that every prime expressed as Mp = 2p − 1 has a corresponding perfect number Mp × (Mp+1)/2 = 2p − 1 × (2p − 1). For example, the Mersenne prime 22 − 1 = 3 leads to the corresponding perfect number 22 − 1 × (22 − 1) = 2 × 3 = 6. In 1747, Leonhard Euler completed what is now called the Euclid–Euler theorem, showing that these are the only even perfect numbers. As a result, there is a one-to-one correspondence between Mersenne primes and even perfect numbers, so a list of one can be converted into a list of the other.[1][5][6]
It is currently an open problem whether there are infinitely many Mersenne primes and even perfect numbers.[2][6] The density of Mersenne primes is the subject of the Lenstra–Pomerance–Wagstaff conjecture, which states that the expected number of Mersenne primes less than some given x is (eγ / log 2) × log log x, where e is Euler's number, γ is Euler's constant, and log is the natural logarithm.[7][8][9] It is widely believed,[10] but not proven, that no odd perfect numbers exist; numerous restrictive conditions have been proven,[10] including a lower bound of 101500.[11]
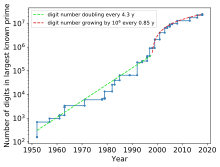
The following is a list of all 52 currently known (as of January 2025[update]) Mersenne primes and corresponding perfect numbers, along with their exponents p. The largest 18 of these have been discovered by the distributed computing project Great Internet Mersenne Prime Search, or GIMPS; their discoverers are listed as "GIMPS / name", where the name is the person who supplied the computer that made the discovery.[2] New Mersenne primes are found using the Lucas–Lehmer test (LLT), a primality test for Mersenne primes that is efficient for binary computers.[2] Due to this efficiency, the largest known prime number has often been a Mersenne prime.[12]
All possible exponents up to the 48th (p = 57,885,161) have been tested and verified by GIMPS as of October 2021[update].[13] Ranks 49 and up are provisional, and may change in the unlikely event that additional primes are discovered between the currently listed ones. Later entries are extremely long, so only the first and last six digits of each number are shown, along with the number of decimal digits.
| Rank | p | Mersenne prime | Perfect number | Discovery | Ref.[14] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Value | Digits | Value | Digits | Date | Discoverer | Method | |||
| 1 | 2 | 3 | 1 | 6 | 1 | Ancient times[a] |
Known to Ancient Greek mathematicians | Unrecorded | [15][16][17] |
| 2 | 3 | 7 | 1 | 28 | 2 | [15][16][17] | |||
| 3 | 5 | 31 | 2 | 496 | 3 | [15][16][17] | |||
| 4 | 7 | 127 | 3 | 8128 | 4 | [15][16][17] | |||
| 5 | 13 | 8191 | 4 | 33550336 | 8 | 13th century or 1456[b] |
Ibn Fallus or anonymous[c] | Trial division | [16][17] |
| 6 | 17 | 131071 | 6 | 8589869056 | 10 | 1588[b] | Pietro Cataldi | [2][20] | |
| 7 | 19 | 524287 | 6 | 137438691328 | 12 | [2][20] | |||
| 8 | 31 | 2147483647 | 10 | 230584...952128 | 19 | 1772 | Leonhard Euler | Trial division with modular restrictions | [21][22] |
| 9 | 61 | 230584...693951 | 19 | 265845...842176 | 37 | Nov 1883 | Ivan Pervushin | Lucas sequences | [23] |
| 10 | 89 | 618970...562111 | 27 | 191561...169216 | 54 | Jun 1911 | Ralph Ernest Powers | [24] | |
| 11 | 107 | 162259...288127 | 33 | 131640...728128 | 65 | Jun 1, 1914 | [25] | ||
| 12 | 127 | 170141...105727 | 39 | 144740...152128 | 77 | Jan 10, 1876 | Édouard Lucas | [26] | |
| 13 | 521 | 686479...057151 | 157 | 235627...646976 | 314 | Jan 30, 1952 | Raphael M. Robinson | Lucas–Lehmer test (LLT) on SWAC | [27] |
| 14 | 607 | 531137...728127 | 183 | 141053...328128 | 366 | [27] | |||
| 15 | 1,279 | 104079...729087 | 386 | 541625...291328 | 770 | Jun 25, 1952 | [28] | ||
| 16 | 2,203 | 147597...771007 | 664 | 108925...782528 | 1,327 | Oct 7, 1952 | [29] | ||
| 17 | 2,281 | 446087...836351 | 687 | 994970...915776 | 1,373 | Oct 9, 1952 | [29] | ||
| 18 | 3,217 | 259117...315071 | 969 | 335708...525056 | 1,937 | Sep 8, 1957 | Hans Riesel | LLT on BESK | [30] |
| 19 | 4,253 | 190797...484991 | 1,281 | 182017...377536 | 2,561 | Nov 3, 1961 | Alexander Hurwitz | LLT on IBM 7090 | [31] |
| 20 | 4,423 | 285542...580607 | 1,332 | 407672...534528 | 2,663 | [31] | |||
| 21 | 9,689 | 478220...754111 | 2,917 | 114347...577216 | 5,834 | May 11, 1963 | Donald B. Gillies | LLT on ILLIAC II | [32] |
| 22 | 9,941 | 346088...463551 | 2,993 | 598885...496576 | 5,985 | May 16, 1963 | [32] | ||
| 23 | 11,213 | 281411...392191 | 3,376 | 395961...086336 | 6,751 | Jun 2, 1963 | [32] | ||
| 24 | 19,937 | 431542...041471 | 6,002 | 931144...942656 | 12,003 | Mar 4, 1971 | Bryant Tuckerman | LLT on IBM 360/91 | [33] |
| 25 | 21,701 | 448679...882751 | 6,533 | 100656...605376 | 13,066 | Oct 30, 1978 | Landon Curt Noll & Laura Nickel | LLT on CDC Cyber 174 | [34] |
| 26 | 23,209 | 402874...264511 | 6,987 | 811537...666816 | 13,973 | Feb 9, 1979 | Landon Curt Noll | [34] | |
| 27 | 44,497 | 854509...228671 | 13,395 | 365093...827456 | 26,790 | Apr 8, 1979 | Harry L. Nelson & David Slowinski | LLT on Cray-1 | [35][36] |
| 28 | 86,243 | 536927...438207 | 25,962 | 144145...406528 | 51,924 | Sep 25, 1982 | David Slowinski | [37] | |
| 29 | 110,503 | 521928...515007 | 33,265 | 136204...862528 | 66,530 | Jan 29, 1988 | Walter Colquitt & Luke Welsh | LLT on NEC SX-2 | [38][39] |
| 30 | 132,049 | 512740...061311 | 39,751 | 131451...550016 | 79,502 | Sep 19, 1983 | David Slowinski et al. (Cray) | LLT on Cray X-MP | [40] |
| 31 | 216,091 | 746093...528447 | 65,050 | 278327...880128 | 130,100 | Sep 1, 1985 | LLT on Cray X-MP/24 | [41][42] | |
| 32 | 756,839 | 174135...677887 | 227,832 | 151616...731328 | 455,663 | Feb 17, 1992 | LLT on Harwell Lab's Cray-2 | [43] | |
| 33 | 859,433 | 129498...142591 | 258,716 | 838488...167936 | 517,430 | Jan 4, 1994 | LLT on Cray C90 | [44] | |
| 34 | 1,257,787 | 412245...366527 | 378,632 | 849732...704128 | 757,263 | Sep 3, 1996 | LLT on Cray T94 | [45][46] | |
| 35 | 1,398,269 | 814717...315711 | 420,921 | 331882...375616 | 841,842 | Nov 13, 1996 | GIMPS / Joel Armengaud | LLT / Prime95 on 90 MHz Pentium PC | [47] |
| 36 | 2,976,221 | 623340...201151 | 895,932 | 194276...462976 | 1,791,864 | Aug 24, 1997 | GIMPS / Gordon Spence | LLT / Prime95 on 100 MHz Pentium PC | [48] |
| 37 | 3,021,377 | 127411...694271 | 909,526 | 811686...457856 | 1,819,050 | Jan 27, 1998 | GIMPS / Roland Clarkson | LLT / Prime95 on 200 MHz Pentium PC | [49] |
| 38 | 6,972,593 | 437075...193791 | 2,098,960 | 955176...572736 | 4,197,919 | Jun 1, 1999 | GIMPS / Nayan Hajratwala | LLT / Prime95 on IBM Aptiva with 350 MHz Pentium II processor | [50] |
| 39 | 13,466,917 | 924947...259071 | 4,053,946 | 427764...021056 | 8,107,892 | Nov 14, 2001 | GIMPS / Michael Cameron | LLT / Prime95 on PC with 800 MHz Athlon T-Bird processor | [51] |
| 40 | 20,996,011 | 125976...682047 | 6,320,430 | 793508...896128 | 12,640,858 | Nov 17, 2003 | GIMPS / Michael Shafer | LLT / Prime95 on Dell Dimension PC with 2 GHz Pentium 4 processor | [52] |
| 41 | 24,036,583 | 299410...969407 | 7,235,733 | 448233...950528 | 14,471,465 | May 15, 2004 | GIMPS / Josh Findley | LLT / Prime95 on PC with 2.4 GHz Pentium 4 processor | [53] |
| 42 | 25,964,951 | 122164...077247 | 7,816,230 | 746209...088128 | 15,632,458 | Feb 18, 2005 | GIMPS / Martin Nowak | [54] | |
| 43 | 30,402,457 | 315416...943871 | 9,152,052 | 497437...704256 | 18,304,103 | Dec 15, 2005 | GIMPS / Curtis Cooper & Steven Boone | LLT / Prime95 on PC at University of Central Missouri | [55] |
| 44 | 32,582,657 | 124575...967871 | 9,808,358 | 775946...120256 | 19,616,714 | Sep 4, 2006 | [56] | ||
| 45 | 37,156,667 | 202254...220927 | 11,185,272 | 204534...480128 | 22,370,543 | Sep 6, 2008 | GIMPS / Hans-Michael Elvenich | LLT / Prime95 on PC | [57] |
| 46 | 42,643,801 | 169873...314751 | 12,837,064 | 144285...253376 | 25,674,127 | Jun 4, 2009[d] | GIMPS / Odd Magnar Strindmo | LLT / Prime95 on PC with 3 GHz Intel Core 2 processor | [58] |
| 47 | 43,112,609 | 316470...152511 | 12,978,189 | 500767...378816 | 25,956,377 | Aug 23, 2008 | GIMPS / Edson Smith | LLT / Prime95 on Dell OptiPlex PC with Intel Core 2 Duo E6600 processor | [57][59][60] |
| 48 | 57,885,161 | 581887...285951 | 17,425,170 | 169296...130176 | 34,850,340 | Jan 25, 2013 | GIMPS / Curtis Cooper | LLT / Prime95 on PC at University of Central Missouri | [61][62] |
| * | 71,344,193 | Lowest unverified milestone[e] | |||||||
| 49[f] | 74,207,281 | 300376...436351 | 22,338,618 | 451129...315776 | 44,677,235 | Jan 7, 2016[g] | GIMPS / Curtis Cooper | LLT / Prime95 on PC with Intel Core i7-4790 processor | [63][64] |
| 50[f] | 77,232,917 | 467333...179071 | 23,249,425 | 109200...301056 | 46,498,850 | Dec 26, 2017 | GIMPS / Jonathan Pace | LLT / Prime95 on PC with Intel Core i5-6600 processor | [65][66] |
| 51[f] | 82,589,933 | 148894...902591 | 24,862,048 | 110847...207936 | 49,724,095 | Dec 7, 2018 | GIMPS / Patrick Laroche | LLT / Prime95 on PC with Intel Core i5-4590T processor | [67][68] |
| * | 128,461,759 | Lowest untested milestone[e] | |||||||
| 52[f] | 136,279,841 | 881694...871551 | 41,024,320 | 388692...008576 | 82,048,640 | Oct 12, 2024 | GIMPS / Luke Durant | LLT / PRPLL on Nvidia H100 GPU[h] | [69] |
Notes
[edit]- ^ The first four perfect numbers were documented by Nicomachus circa 100, and the concept was known (along with corresponding Mersenne primes) to Euclid at the time of his Elements. There is no record of discovery.
- ^ a b Islamic mathematicians such as Ismail ibn Ibrahim ibn Fallus (1194–1239) may have known of the fifth through seventh perfect numbers prior to European records.[18]
- ^ Found in an anonymous manuscript designated Clm 14908, dated 1456 and 1461. Ibn Fallus' earlier work in the 13th century also mentioned the prime, but was not widely distributed.[16][19]
- ^ M42,643,801 was first reported to GIMPS on April 12, 2009, but was not noticed by a human until June 4, 2009, due to a server error.
- ^ a b As of 21 January 2025[update].[13] All exponents below the lowest unverified milestone have been checked more than once. All exponents below the lowest untested milestone have been checked at least once.
- ^ a b c d It has not been verified whether any undiscovered Mersenne primes exist between the 48th (M57,885,161) and the 52nd (M136,279,841) on this table; the ranking is therefore provisional.
- ^ M74,207,281 was first reported to GIMPS on September 17, 2015 but was not noticed by a human until January 7, 2016 due to a server error.
- ^ First detected as a probable prime using Fermat primality test on an Nvidia A100 GPU on October 11, 2024
References
[edit]- ^ a b Stillwell, John (2010). Mathematics and Its History. Undergraduate Texts in Mathematics. Springer Science+Business Media. p. 40. ISBN 978-1-4419-6052-8. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ a b c d e f g Caldwell, Chris K. "Mersenne Primes: History, Theorems and Lists". PrimePages. Archived from the original on 4 October 2021. Retrieved 4 October 2021.
- ^ Caldwell, Chris K. "If 2n-1 is prime, then so is n". PrimePages. Archived from the original on 5 October 2021. Retrieved 12 October 2021.
- ^ Prielipp, Robert W. (1970). "Perfect Numbers, Abundant Numbers, and Deficient Numbers". The Mathematics Teacher. 63 (8): 692–96. doi:10.5951/MT.63.8.0692. JSTOR 27958492. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ Caldwell, Chris K. "Characterizing all even perfect numbers". PrimePages. Archived from the original on 8 October 2014. Retrieved 12 October 2021.
- ^ a b Crilly, Tony (2007). "Perfect numbers". 50 mathematical ideas you really need to know. Quercus Publishing. ISBN 978-1-84724-008-8. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ Caldwell, Chris K. "Heuristics Model for the Distribution of Mersennes". PrimePages. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ Wagstaff, Samuel S. (January 1983). "Divisors of Mersenne numbers". Mathematics of Computation. 40 (161): 385–397. doi:10.1090/S0025-5718-1983-0679454-X. ISSN 0025-5718.
- ^ Pomerance, Carl (September 1981). "Recent developments in primality testing" (PDF). The Mathematical Intelligencer. 3 (3): 97–105. doi:10.1007/BF03022861. ISSN 0343-6993. S2CID 121750836.
- ^ a b Nadis, Steve (10 September 2020). "Mathematicians Open a New Front on an Ancient Number Problem". Quanta Magazine.
Like many of his 21st-century peers, Nielsen thinks there probably aren't any OPNs. And, also like his peers, he does not believe a proof is within immediate reach.
- ^ Ochem, Pascal; Rao, Michaël (30 January 2012). "Odd perfect numbers are greater than 101500". Mathematics of Computation. 81 (279): 1869–1877. doi:10.1090/S0025-5718-2012-02563-4. ISSN 0025-5718.
- ^ Caldwell, Chris K. "The Largest Known prime by Year: A Brief History". PrimePages. Archived from the original on 4 October 2021. Retrieved 13 October 2021.
- ^ a b "GIMPS Milestones Report". Great Internet Mersenne Prime Search. Archived from the original on 13 October 2021. Retrieved 31 January 2024.
- ^ Sources applying to almost all entries:
- "List of Known Mersenne Prime Numbers". Great Internet Mersenne Prime Search. Archived from the original on 7 June 2020. Retrieved 4 October 2021.
- Caldwell, Chris K. "Mersenne Primes: History, Theorems and Lists". PrimePages. Archived from the original on 4 October 2021. Retrieved 4 October 2021.
- Caldwell, Chris K. "The Largest Known prime by Year: A Brief History". PrimePages. Archived from the original on 4 October 2021. Retrieved 13 October 2021.
- Haworth, Guy M. (1987). Mersenne numbers (PDF) (Report). Archived (PDF) from the original on 13 October 2021. Retrieved 13 October 2021.
- Noll, Landon Curt (21 December 2018). "Known Mersenne Primes". Archived from the original on 27 July 2021. Retrieved 13 October 2021.
- Tattersall, James J. (1999). Elementary Number Theory in Nine Chapters. Cambridge University Press. pp. 131–134. ISBN 978-0-521-58531-6. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ a b c d Joyce, David E. "Euclid's Elements, Book IX, Proposition 36". mathcs.clarku.edu. Archived from the original on 17 June 2021. Retrieved 13 October 2021.
- ^ a b c d e f Dickson, Leonard Eugene (1919). History of the Theory of Numbers, Vol. I. Carnegie Institution of Washington. pp. 4–6. Archived from the original on 2023-04-08. Retrieved 2023-03-19.
- ^ a b c d e Smith, David Eugene (1925). History of Mathematics: Volume II. Dover. p. 21. ISBN 978-0-486-20430-7.
- ^ O'Connor, John J.; Robertson, Edmund F. "Perfect numbers". MacTutor History of Mathematics archive. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ "'Calendarium ecclesiasticum – BSB Clm 14908'". Bavarian State Library. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ a b Cataldi, Pietro Antonio (1603). Trattato de' numeri perfetti di Pietro Antonio Cataldo [Pietro Antonio Cataldi's treatise on perfect numbers] (in Italian). Presso di Heredi di Giouanni Rossi. Archived from the original on 2023-04-05. Retrieved 2023-03-19.
- ^ Caldwell, Chris K. "Modular restrictions on Mersenne divisors". PrimePages. Archived from the original on 11 November 2021. Retrieved 22 November 2021.
- ^ Euler, Leonhard (1772). "Extrait d'un lettre de M. Euler le pere à M. Bernoulli concernant le Mémoire imprimé parmi ceux de 1771, p 318" [Extract of a letter from Mr. Euler to Mr. Bernoulli, concerning the Mémoire published among those of 1771]. Nouveaux Mémoires de l'académie royale des sciences de Berlin (in French). 1772: 35–36. Archived from the original on 15 August 2020. Retrieved 13 October 2021 – via Euler Archive.
- ^ "Sur un nouveau nombre premier, annoncé par le père Pervouchine" [On a new prime number, announced by Pervouchine]. Bulletin de l'Académie impériale des sciences de St.-Pétersbourg (in French). 31: 532–533. 27 January 1887. Archived from the original on 13 October 2021. Retrieved 13 October 2021 – via Biodiversity Heritage Library.
- ^ Powers, R. E. (November 1911). "The Tenth Perfect Number". The American Mathematical Monthly. 18 (11): 195–197. doi:10.2307/2972574. JSTOR 2972574.
- ^ "Records of Proceedings at Meetings". Proceedings of the London Mathematical Society. s2-13 (1): iv–xl. 1914. doi:10.1112/plms/s2-13.1.1-s.
- ^ Lucas, Édouard (1876). "Note sur l'application des séries récurrentes à la recherche de la loi de distribution des nombres premiers" [Note on the application of recurrent series to researching the law of prime number distribution]. Comptes rendus de l'Académie des Sciences (in French). 82: 165–167. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ a b "Notes". Mathematics of Computation. 6 (37): 58–61. January 1952. doi:10.1090/S0025-5718-52-99405-2. ISSN 0025-5718. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
- ^ "Notes". Mathematics of Computation. 6 (39): 204–205. July 1952. doi:10.1090/S0025-5718-52-99389-7. ISSN 0025-5718.
- ^ a b "Notes". Mathematics of Computation. 7 (41): 67–72. January 1953. doi:10.1090/S0025-5718-53-99372-7. ISSN 0025-5718.
- ^ Riesel, Hans (January 1958). "A New Mersenne Prime". Mathematics of Computation. 12 (61): 60. doi:10.1090/S0025-5718-58-99282-2. Archived from the original on 2021-10-28. Retrieved 2021-10-13.
- ^ a b Hurwitz, Alexander (April 1962). "New Mersenne primes". Mathematics of Computation. 16 (78): 249–251. doi:10.1090/S0025-5718-1962-0146162-X. ISSN 0025-5718.
- ^ a b c Gillies, Donald B. (January 1964). "Three new Mersenne primes and a statistical theory". Mathematics of Computation. 18 (85): 93–97. doi:10.1090/S0025-5718-1964-0159774-6. JSTOR 2003409.
- ^ Tuckerman, Bryant (October 1971). "The 24th Mersenne Prime". Proceedings of the National Academy of Sciences. 68 (10): 2319–2320. Bibcode:1971PNAS...68.2319T. doi:10.1073/pnas.68.10.2319. PMC 389411. PMID 16591945.
- ^ a b Noll, Landon Curt; Nickel, Laura (October 1980). "The 25th and 26th Mersenne primes". Mathematics of Computation. 35 (152): 1387. doi:10.1090/S0025-5718-1980-0583517-4. JSTOR 2006405.
- ^ Slowinski, David (1978). "Searching for the 27th Mersenne prime". Journal of Recreational Mathematics. 11 (4): 258–261.
- ^ "Science Watch: A New Prime Number". The New York Times. 5 June 1979. Archived from the original on 2 November 2021. Retrieved 13 October 2021.
- ^ "Announcements". The Mathematical Intelligencer. 5 (1): 60. March 1983. doi:10.1007/BF03023507. ISSN 0343-6993.
- ^ Peterson, I. (6 February 1988). "Priming for a Lucky Strike". Science News. 133 (6): 85. doi:10.2307/3972461. JSTOR 3972461.
- ^ Colquitt, W. N.; Welsh, L. (April 1991). "A new Mersenne prime". Mathematics of Computation. 56 (194): 867. Bibcode:1991MaCom..56..867C. doi:10.1090/S0025-5718-1991-1068823-9. JSTOR 2008415.
- ^ "Number is largest prime found yet". The Globe and Mail. 24 September 1983. ProQuest 386439660. Archived from the original on 2 November 2021. Retrieved 7 January 2022 – via ProQuest.
- ^ Peterson, I. (28 September 1985). "Prime Time for Supercomputers". Science News. 128 (13): 199. doi:10.2307/3970245. JSTOR 3970245.
- ^ Dembart, Lee (17 September 1985). "Supercomputer Comes Up With Whopping Prime Number". Los Angeles Times. Archived from the original on 2 November 2021. Retrieved 13 October 2021.
- ^ Maddox, John (26 March 1992). "The endless search for primality". Nature. 356 (6367): 283. Bibcode:1992Natur.356..283M. doi:10.1038/356283a0. ISSN 1476-4687. S2CID 4327045.
- ^ "Largest Known Prime Number Discovered on Cray Research Supercomputer". PR Newswire. 10 January 1994. Archived from the original on 4 November 2021. Retrieved 21 August 2023 – via Gale.
- ^ Caldwell, Chris K. "A Prime of Record Size! 21257787-1". PrimePages. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ Gillmor, Dan (3 September 1996). "Crunching numbers: Researchers come up with prime math discovery". Knight Ridder – via Gale.
- ^ "GIMPS Discovers 35th Mersenne Prime, 21,398,269-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 12 November 1996. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 36th Mersenne Prime, 22,976,221-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 1 September 1997. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 37th Mersenne Prime, 23,021,377-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 2 February 1998. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 38th Mersenne Prime 26,972,593-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 30 June 1999. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 39th Mersenne Prime, 213,466,917-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 6 December 2001. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 40th Mersenne Prime, 220,996,011-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 2 February 2003. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 41st Mersenne Prime, 224,036,583-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 28 May 2004. Archived from the original on 29 January 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 42nd Mersenne Prime, 225,964,951-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 27 February 2005. Archived from the original on 14 March 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 43rd Mersenne Prime, 230,402,457-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 24 December 2005. Archived from the original on 14 March 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 44th Mersenne Prime, 232,582,657-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 11 September 2006. Archived from the original on 26 January 2021. Retrieved 13 October 2021.
- ^ a b "GIMPS Discovers 45th and 46th Mersenne Primes, 243,112,609-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 15 September 2008. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers 47th Mersenne Prime". Great Internet Mersenne Prime Search. 12 April 2009. Archived from the original on 19 February 2021. Retrieved 13 October 2021.
- ^ Maugh, Thomas H. (27 September 2008). "Rare prime number found". Los Angeles Times. Archived from the original on 27 July 2021. Retrieved 13 October 2021.
- ^ Smith, Edson. "The UCLA Mersenne Prime". UCLA Mathematics. Archived from the original on 22 November 2021. Retrieved 22 November 2021.
- ^ "GIMPS Discovers 48th Mersenne Prime, 257,885,161-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 5 February 2013. Archived from the original on 26 January 2021. Retrieved 13 October 2021.
- ^ Yirka, Bob (6 February 2013). "University professor discovers largest prime number to date". phys.org. Archived from the original on 16 January 2021. Retrieved 13 October 2021.
- ^ "GIMPS Project Discovers Largest Known Prime Number: 274,207,281-1". Great Internet Mersenne Prime Search. 19 January 2016. Archived from the original on 7 January 2018. Retrieved 13 October 2021.
- ^ "Largest known prime number discovered in Missouri". BBC News. 20 January 2016. Archived from the original on 21 August 2021. Retrieved 13 October 2021.
- ^ "GIMPS Project Discovers Largest Known Prime Number: 277,232,917-1". Great Internet Mersenne Prime Search. 3 January 2018. Archived from the original on 4 January 2018. Retrieved 13 October 2021.
- ^ Lamb, Evelyn (4 January 2018). "Why You Should Care About a Prime Number That's 23,249,425 Digits Long". Slate Magazine. Archived from the original on 9 October 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers Largest Known Prime Number: 282,589,933-1". Great Internet Mersenne Prime Search. 21 December 2018. Archived from the original on 22 December 2018. Retrieved 13 October 2021.
- ^ Palca, Joe (21 December 2018). "The World Has A New Largest-Known Prime Number". NPR. Archived from the original on 30 July 2021. Retrieved 13 October 2021.
- ^ "GIMPS Discovers Largest Known Prime Number: 2136,279,841-1". Great Internet Mersenne Prime Search. 21 October 2024. Retrieved 21 October 2024.
External links
[edit]- OEIS sequence A000043 (Corresponding exponents p)
- OEIS sequence A000396 (Perfect numbers)
- OEIS sequence A000668 (Mersenne primes)
- List on GIMPS, with the full values of large numbers Archived 2020-06-07 at the Wayback Machine
- A technical report on the history of Mersenne numbers, by Guy Haworth Archived 2021-10-13 at the Wayback Machine
