User:19sully96/sandbox

Free energy, ensemble averages, and exact differentials

• The partial derivatives of the function F(N, V, T) give important canonical ensemble average quantities:
  • the average pressure is

    $\langle p\rangle =-{\frac {\partial F}{\partial V}},$

  • the Gibbs entropy is
    $S=-k\langle \log P\rangle =-{\frac {\partial F}{\partial T}},$
  • the partial derivative ∂F/∂N is approximately related to chemical potential, although the concept of chemical equilibrium does not exactly apply to canonical ensembles of small systems.
  • and the average energy is
    $\langle E\rangle =F+ST.$
• Exact differential: From the above expressions, it can be seen that the function F(V, T), for a given N, has the exact differential
  $dF=-SdT-\langle p\rangle dV.$
• First law of thermodynamics: Substituting the above relationship for ⟨E⟩ into the exact differential of F, an equation similar to the first law of thermodynamics is found, except with average signs on some of the quantities:
  $d\langle E\rangle =TdS-\langle p\rangle dV.$
• Energy fluctuations: The energy in the system has uncertainty in the canonical ensemble.
  • The variance of the energy is

    $\sigma _{E}^{2}=\langle E^{2}\rangle -\langle E\rangle ^{2}=kT^{2}{\frac {\partial \langle E\rangle }{\partial T}}.$

  • The standard deviation of the energy is related to the heat capacity $C={\frac {\partial \langle E\rangle }{\partial T}}$ by
    $\sigma _{E}=kT{\sqrt {\frac {C}{k}}}.$
  • The relative energy fluctuations decrease with system size by extensivity since ⟨E⟩ ∝ N and C ∝ N, giving
    ${\frac {\sigma _{E}}{\langle E\rangle }}={\frac {kT}{\langle E\rangle }}{\sqrt {\frac {C}{k}}}\propto {\frac {1}{\sqrt {N}}}.$

Boltzmann edits

This page is about system energy states. For particle energy levels and velocities, see Maxwell–Boltzmann distribution.

Boltzmann factor p_i / p_j (vertical axis) as a function of temperature T for several energy differences ε_i − ε_j.

In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution) is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. It is also a frequency distribution of particles in a system. The distribution is expressed in the form

$p_{i}\propto e^{-{\frac {\varepsilon _{i}}{kT}}}$

where p_i is the probability of the system being in state i, ε_i is the energy of that state, and a constant kT of the distribution is the product of Boltzmann's constant k and thermodynamic temperature T. The symbol ${\textstyle \propto }$ denotes proportionality (see § The distribution for the proportionality constant).

The term system here has a very wide meaning; it can range from a single atom to a macroscopic system such as a natural gas storage tank. Because of this the Boltzmann distribution can be used to solve a very wide variety of problems. The distribution shows that states with lower energy will always have a higher probability of being occupied than the states with higher energy.

The ratio of probabilities of two states is known as the Boltzmann factor and characteristically only depends on the states' energy difference:

${\frac {p_{i}}{p_{j}}}=e^{\frac {\varepsilon _{j}-\varepsilon _{i}}{kT}}$

The Boltzmann distribution is named after Ludwig Boltzmann who first formulated it in 1868 during his studies of the statistical mechanics of gases in thermal equilibrium. Boltzmann's statistical work is borne out in his paper “On the Relationship between the Second Fundamental Theorem of the Mechanical Theory of Heat and Probability Calculations Regarding the Conditions for Thermal Equilibrium" The distribution was later investigated extensively, in its modern generic form, by Josiah Willard Gibbs in 1902.

The Boltzmann distribution should not be confused with the Maxwell–Boltzmann distribution. The former gives the probability that a system will be in a certain state as a function of that state's energy; in contrast, the latter is used to describe particle speeds in idealized gases.

The distribution

The Boltzmann distribution is a probability distribution that gives the probability of a certain state as a function of that state's energy and temperature of the system to which the distribution is applied. It is given as

$p_{i}={\frac {1}{Q}}}{e^{-{\varepsilon }_{i}/kT}={\frac {e^{-{\varepsilon }_{i}/kT}}{\sum _{j=1}^{M}{e^{-{\varepsilon }_{j}/kT}}}}$

where p_i is the probability of state i, ε_i the energy of state i, k the Boltzmann constant, T the temperature of the system and M is the number of all states accessible to the system of interest. Implied parentheses around the denominator kT are omitted for brevity. The normalization denominator Q (denoted by some authors by Z) is the canonical partition function

$Q={\sum _{i=1}^{M}{e^{-{\varepsilon }_{i}/kT}}}$

It results from the constraint that the probabilities of all accessible states must add up to 1.

The Boltzmann distribution is the distribution that maximizes the entropy

$H(p_{1},p_{2},\cdots ,p_{M})=-\sum _{i=1}^{M}p_{i}\log _{2}p_{i}$

subject to the constraint that ${\textstyle {\sum {p_{i}{\varepsilon }_{i}}}}$ equals a particular mean energy value (which can be proven using Lagrange multipliers).

The partition function can be calculated if we know the energies of the states accessible to the system of interest. For atoms the partition function values can be found in the NIST Atomic Spectra Database.

The distribution shows that states with lower energy will always have a higher probability of being occupied than the states with higher energy. It can also give us the quantitative relationship between the probabilities of the two states being occupied. The ratio of probabilities for states i and j is given as

${\frac {p_{i}}{p_{j}}}=e^{({\varepsilon }_{j}-{\varepsilon }_{i})/kT}$

Ratios of hydrogen excited states to the ground state in solar atmospheres versus temperature. The fraction of atoms in one state versus another as a function of temperature is given by a Boltzmann factor where the energies correspond to the energy levels of the hydrogen atom. For the sun, at a temperature of about 5800 K, the fraction of hydrogen in the first excited state compared to the ground state is $10^{-9}$, meaning that for every billion atoms in the ground state there is one atom in the first excited state. This is particularly useful in understanding the strength of stellar spectral lines, however, to gain a full understanding of spectral lines one needs to take into account ionization. To do this, the Saha ionization equation is needed.

where p_i is the probability of state i, p_j the probability of state j, and ε_i and ε_j are the energies of states i and j, respectively.

The Boltzmann distribution is often used to describe the distribution of particles, such as atoms or molecules, over energy states accessible to them. If we have a system consisting of many particles, the probability of a particle being in state i is practically the probability that, if we pick a random particle from that system and check what state it is in, we will find it is in state i. This probability is equal to the number of particles in state i divided by the total number of particles in the system, that is the fraction of particles that occupy state i.

$p_{i}={\frac {N_{i}}{N}}$

where N_i is the number of particles in state i and N is the total number of particles in the system. We may use the Boltzmann distribution to find this probability that is, as we have seen, equal to the fraction of particles that are in state i. So the equation that gives the fraction of particles in state i as a function of the energy of that state is

${\frac {N_{i}}{N}}={\frac {e^{-{\varepsilon }_{i}/kT}}{\sum _{j=1}^{M}{e^{-{\varepsilon }_{j}/kT}}}}$

This equation is of great importance to spectroscopy. In spectroscopy we observe a spectral line of atoms or molecules that we are interested in going from one state to another. In order for this to be possible, there must be some particles in the first state to undergo the transition. We may find that this condition is fulfilled by finding the fraction of particles in the first state. If it is negligible, the transition is very likely not to be observed at the temperature for which the calculation was done. In general, a larger fraction of molecules in the first state means a higher number of transitions to the second state. This gives a stronger spectral line. However, there are other factors that influence the intensity of a spectral line, such as whether it is caused by an allowed or a forbidden transition.

The Boltzmann distribution is related to the softmax function commonly used in machine learning.

Category:Statistical mechanics

Ideal gas law edits

Isotherms of an ideal gas. The curved lines represent the relationship between pressure (on the vertical axis) and volume (on the horizontal axis) for an ideal gas at different temperatures: lines that are farther away from the origin (that is, lines that are nearer to the top right-hand corner of the diagram) represent higher temperatures.

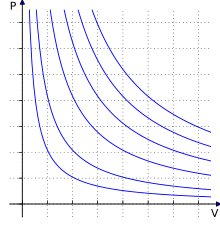
Derivations

Empirical

The empirical laws that led to the derivation of the ideal gas law were discovered with experiments that changed only 2 state variables of the gas and kept every other one constant.

All the possible gas laws that could have been discovered with this kind of setup are:

${PV}=C_{1}$ or $P_{1}V_{1}=P_{2}V_{2}$ (1) known as Boyle's law

${\frac {V}{T}}=C_{2}$ or ${\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}$ (2) known as Charles's law

${\frac {V}{N}}=C_{3}$ or ${\frac {V_{1}}{N_{1}}}={\frac {V_{2}}{N_{2}}}$ (3) known as Avogadro's law

${\frac {P}{T}}=C_{4}$or ${\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}$ (4) known as Gay-Lussac's law

$NT=C_{5}$or $N_{1}T_{1}=N_{2}T_{2}$ (5)

${\frac {P}{N}}=C_{6}$ or ${\frac {P_{1}}{N_{1}}}={\frac {P_{2}}{N_{2}}}$ (6)

Relationships between Boyle's, Charles's, Gay-Lussac's, Avogadro's, combined and ideal gas laws, with the Boltzmann constant k = R/N_A = n R/N (in each law, properties circled are variable and properties not circled are held constant)

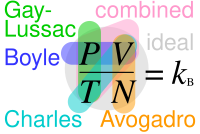
Where "P" stands for pressure, "V" for volume, "N" for number of particles in the gas and "T" for temperature; Where $C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}$ are not actual constants but are in this context because of each equation requiring only the parameters explicitly noted in it changing.

To derive the ideal gas law one does not need to know all 6 formulas, one can just know 3 and with those derive the rest or just one more to be able to get the ideal gas law, which needs 4.

Since each formula only holds when only the state variables involved in said formula change while the others remain constant, we cannot simply use algebra and directly combine them all. I.e. Boyle did his experiments while keeping N and T constant and this must be taken into account.

Keeping this in mind, to carry the derivation on correctly, one must imagine the gas being altered by one process at a time. The derivation using 4 formulas can look like this:

at first the gas has parameters $P_{1},V_{1},N_{1},T_{1}$

Say, starting to change only pressure and volume, according to Boyle's law, then:

$P_{1}V_{1}=P_{2}V_{2}$ (7) After this process, the gas has parameters $P_{2},V_{2},N_{1},T_{1}$

Using then Eq. (5) to change the number of particles in the gas and the temperature,

$N_{1}T_{1}=N_{2}T_{2}$ (8) After this process, the gas has parameters $P_{2},V_{2},N_{2},T_{2}$

Using then Eq. (6) to change the pressure and the number of particles,

${\frac {P_{2}}{N_{2}}}={\frac {P_{3}}{N_{3}}}$ (9) After this process, the gas has parameters $P_{3},V_{2},N_{3},T_{2}$

Using then Charles's law to change the volume and temperature of the gas,

${\frac {V_{2}}{T_{2}}}={\frac {V_{3}}{T_{3}}}$ (10) After this process, the gas has parameters $P_{3},V_{3},N_{3},T_{3}$

Using simple algebra on equations (7), (8), (9) and (10) yields the result:

${\frac {P_{1}V_{1}}{N_{1}T_{1}}}={\frac {P_{3}V_{3}}{N_{3}T_{3}}}$ or ${\frac {PV}{NT}}=K_{B}$, Where $K_{B}$ stands for Boltzmann's constant.

Another equivalent result, using the fact that $nR=NK_{B}$ ,where "n" is the number of moles in the gas and "R" is the universal gas constant, is:

$PV=nRT$, which is known as the ideal gas law.

If you know or have found with an experiment 3 of the 6 formulas, you can easily derive the rest using the same method explained above; but due to the properties of said equations, namely that they only have 2 variables in them, they can't be any 3 formulas. For example, if you were to have Eqs. (1), (2) and (4) you would not be able to get any more because combining any two of them will give you the third; But if you had Eqs. (1), (2) and (3) you would be able to get all 6 Equations without having to do the rest of the experiments because combining (1) and (2) will yield (4), then (1) and (3) will yield (6), then (4) and (6) will yield (5), as well as would the combination of (2) and (3) as is visually explained in the following visual relation:

Relationship between the 6 gas laws

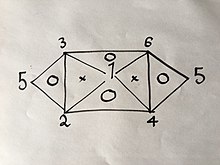
Where the numbers represent the gas laws numbered above.

If you were to use the same method used above on 2 of the 3 laws on the vertices of one triangle that has a "O" inside it, you would get the third.

For example:

Change only pressure and volume first: $P_{1}V_{1}=P_{2}V_{2}$ (1´)

then only volume and temperature: ${\frac {V_{2}}{T_{1}}}={\frac {V_{3}}{T_{2}}}$ (2´)

then as we can choose any value for $V_{3}$, if we set $V_{1}=V_{3}$, Eq. (2´) becomes: ${\frac {V_{2}}{T_{1}}}={\frac {V_{1}}{T_{2}}}$(3´)

combining equations (1´) and (3´) yields ${\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}$ , which is Eq. (4), of which we had no prior knowledge until this derivation.

Theoretical

Kinetic theory

Main article: Kinetic theory of gases

The ideal gas law can also be derived from first principles using the kinetic theory of gases, in which several simplifying assumptions are made, chief among which are that the molecules, or atoms, of the gas are point masses, possessing mass but no significant volume, and undergo only elastic collisions with each other and the sides of the container in which both linear momentum and kinetic energy are conserved.

Statistical mechanics

Main article: Statistical mechanics

Let q = (q_x, q_y, q_z) and p = (p_x, p_y, p_z) denote the position vector and momentum vector of a particle of an ideal gas, respectively. Let F denote the net force on that particle. Then the time-averaged kinetic energy of the particle is:

${\begin{aligned}\langle \mathbf {q} \cdot \mathbf {F} \rangle &={\Bigl \langle }q_{x}{\frac {dp_{x}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{y}{\frac {dp_{y}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{z}{\frac {dp_{z}}{dt}}{\Bigr \rangle }\\&=-{\Bigl \langle }q_{x}{\frac {\partial H}{\partial q_{x}}}{\Bigr \rangle }-{\Bigl \langle }q_{y}{\frac {\partial H}{\partial q_{y}}}{\Bigr \rangle }-{\Bigl \langle }q_{z}{\frac {\partial H}{\partial q_{z}}}{\Bigr \rangle }=-3k_{B}T,\end{aligned}}$

where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of N particles yields

$3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }.$

By Newton's third law and the ideal gas assumption, the net force of the system is the force applied by the walls of the container, and this force is given by the pressure P of the gas. Hence

$-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} ,$

where dS is the infinitesimal area element along the walls of the container. Since the divergence of the position vector q is

$\nabla \cdot \mathbf {q} ={\frac {\partial q_{x}}{\partial q_{x}}}+{\frac {\partial q_{y}}{\partial q_{y}}}+{\frac {\partial q_{z}}{\partial q_{z}}}=3,$

the divergence theorem implies that

$P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} =P\int _{\mathrm {volume} }\left(\nabla \cdot \mathbf {q} \right)dV=3PV,$

where dV is an infinitesimal volume within the container and V is the total volume of the container.

Putting these equalities together yields

$3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=3PV,$

which immediately implies the ideal gas law for N particles:

$PV=Nk_{B}T=nRT,\,$

where n = N/N_A is the number of moles of gas and R = N_Ak_B is the gas constant.

Canonical Ensemble

Main article: Canonical ensemble

Assuming the particles making up the gas are non-interacting with each other, are confined to a fixed volume and are in thermal equilibrium, one can use the tools of the canonical ensemble to derive the ideal gas law. It is also possible to repeat similar derivations using the microcanonical and grand canonical ensembles. This derivation will follow generally the steps given by Kardar in "Statistical Physics of Particles."

The canonical partition function of a system of $N$ classical, identical particles with mass $m$ in a three dimensional box is given by

$Z={\frac {1}{h^{3N}N!}}\int \dots \int e^{-H/kT}d^{3}p_{1}\dots d^{3}q_{N}$,

where $H=\sum _{i=1}^{N}{\bigg (}{\frac {p_{i}^{2}}{2m}}+U(q_{i}){\bigg )}$is the Hamiltonian, $h$ is Planck's constant, and ${\frac {1}{h^{3N}N!}}$ serves as a normalization factor.

Since an ideal gas is assumed to have no interactions between particles, the potential $U$ is just the hard box potential,

$U(q_{i})={\begin{cases}\infty &{\text{if }}q_{i}{\text{ is outside the box}}\\0&{\text{if }}q_{i}{\text{ is inside the box}}\end{cases}}$.

Thus the integral over all of phase space in the partition function reduces to

$Z={\frac {V^{N}}{h^{3N}N!}}\int \dots \int e^{{\big (}-{\frac {1}{kT}}\sum {\frac {p_{i}^{2}}{2m}}{\big )}}d^{3}p_{1}\dots d^{3}p_{N}$

$={\frac {V^{N}}{h^{3N}N!}}\prod _{i=1}^{N}\int e^{{\big (}-{\frac {1}{kT}}{\frac {p_{i}^{2}}{2m}}{\big )}}d^{3}p_{i}={\frac {V^{N}}{h^{3N}N!}}{\bigg [}\int e^{{\big (}-{\frac {1}{kT}}{\frac {p_{1}^{2}}{2m}}{\big )}}d^{3}p_{1}{\bigg ]}^{N}$,

where $V$ is the volume of the box.

The last equality comes from the fact that the particles are identical. Since the integral in the last equality is Gaussian, it is relatively easy to compute.

Defining $\lambda ={\sqrt {\frac {h^{2}}{2\pi mkT}}}$ to be the characteristic length for $h$ at temperature $T$, the partition function reduces further to

$Z={\frac {V^{N}}{h^{3N}N!}}{\bigg [}{\big (}2\pi mkT{\big )}^{\frac {3}{2}}{\bigg ]}^{N}={\frac {1}{N!}}{\bigg (}{\frac {V}{\lambda ^{3}}}{\bigg )}^{N}$.

Now that the canonical partition function of an ideal gas has been calculated, one can solve for the free energy (specifically the Helmholtz free energy) and then use thermodynamics to obtain the ideal gas law.

The free energy is given by

$F=-kT\log {Z}$

$=-NkT\log {\bigg [}{\frac {V}{\lambda ^{3}}}{\bigg ]}+kT\log {{\big [}N!{\big ]}}$

$\approx -NkT\ln {\bigg [}{\frac {V}{\lambda ^{3}}}{\bigg ]}+NkT\ln {{\big [}N{\big ]}}-NkT$,

where the approximation comes from using Stirling's approximation for factorials. Substituting in for $\lambda$ and using simple logarithm rules yields the result

$F=-NkT{\bigg (}\ln {{\bigg [}{\frac {V}{N}}{\bigg ]}}+{\frac {3}{2}}\ln {{\bigg [}{\frac {2\pi mkT}{h^{2}}}{\bigg ]}}+1{\bigg )}$.

Now that the free energy has been calculated, one can use the main thermodynamic identity $dF=-SdT-PdV+\mu dN$and take partial derivatives to obtain the ideal gas law.

Starting with the identity for pressure,

$P=-{\bigg (}{\frac {\partial F}{\partial V}}{\bigg )}_{T,N}=NkT{\bigg (}{\frac {N}{V}}{\bigg )}\cdot {\frac {1}{N}}={\frac {NkT}{V}}$

which is the ideal gas law.

See also

• Van der Waals equation – Gas equation of state which accounts for non-ideal gas behavior
• Boltzmann constant – Physical constant relating particle kinetic energy with temperature
• Configuration integral – Function in thermodynamics and statistical physics
• Dynamic pressure – Kinetic energy per unit volume of a fluid
• Internal energy – Energy contained within a system

Further reading

• Davis; Masten (2002). Principles of Environmental Engineering and Science. New York: McGraw-Hill. ISBN 0-07-235053-9.

External links

• "Website giving credit to Benoît Paul Émile Clapeyron, (1799–1864) in 1834". Archived from the original on July 5, 2007.
• Configuration integral (statistical mechanics) where an alternative statistical mechanics derivation of the ideal-gas law, using the relationship between the Helmholtz free energy and the partition function, but without using the equipartition theorem, is provided. Vu-Quoc, L., Configuration integral (statistical mechanics), 2008. this wiki site is down; see this article in the web archive on 2012 April 28.
• pv=nrt calculator ideal gas law calculator - Engineering Units online calculator
• Gas equations in detail

Category:Gas laws Category:Ideal gas Category:Equations of state Category:1834 introductions