 |
Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review! |
The Tseitin Transformation is used to produce a boolean equation in conjunctive normal form (CNF) from a combinatorial logic circuit so that it may be solved by a SAT solver.
Motivation[edit]
The naive approach is to write the circuit as an equation, and use De Morgan's law and distribution. However, this can result in an exponential increase in equation size. The Tseitin Transformation outputs an equation whose size has grown linearly relative to the input circuit's.
Approach[edit]
The output equation is the constant 1 set equal to an expression. This expression is a conjunction of sub-expressions, where the satisfaction of each sub-expression enforces the proper operation of a single gate in the input circuit. The satisfaction of the entire output expression thus enforces that the entire input circuit is operating properly.
For each gate, a new variable representing its output is introduced. A small pre-calculated CNF expression that relates the inputs and outputs is appended (via the and operation) the output expression. Note that inputs to these gates can be both the original literals, or the introduced variables representing outputs of sub-gates.
A final clause is appended with a single literal: the final gate's output variable. If this literal is complemented, then the satisfaction of this clause enforces the output expression's to false; otherwise the expression is forced true.
Gate Sub-expressions[edit]
Listed is some of the possible sub-expressions that can be created for various logic gates.
| Type |
Operation |
CNF Sub-expression
|
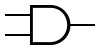 AND AND
|

|

|
 OR OR
|

|

|
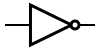 NOT NOT
|

|

|
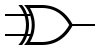 XOR XOR
|

|

|
 NOR NOR
|

|

|
 NAND NAND
|

|

|
Examples[edit]
Simple combinatorial logic[edit]
The following circuit returns true when at least some of its inputs are true, but not more than two at a time. It implements the equation  . A variable is introduced for each gates' output; here each is marked in red:
. A variable is introduced for each gates' output; here each is marked in red:

Notice that the output of the inverter with  as an input has two variables introduced. While this is redundant, it does not affect the equisatisfiability of the resulting equation. Now substitute each gate with its appropriate CNF sub-expression:
as an input has two variables introduced. While this is redundant, it does not affect the equisatisfiability of the resulting equation. Now substitute each gate with its appropriate CNF sub-expression:
| gate
|
CNF sub-expression
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
The final output variable is  so to enforce that the output of this circuit be true, one final simple clause is appended:
so to enforce that the output of this circuit be true, one final simple clause is appended:
 . Combining these equations results in the final instance of SAT:
. Combining these equations results in the final instance of SAT:
One possible satisfying assignment of these variables is:
| variable
|
value
|
| gate2
|
0
|
| gate3
|
1
|
| gate1
|
1
|
| gate6
|
1
|
| gate7
|
0
|
| gate4
|
0
|
| gate5
|
1
|
| gate8
|
1
|
| x2
|
0
|
| x3
|
1
|
| x1
|
0
|
The values of the introduced values are usually discarded, but they can be used to trace the logic path in the original circuit. Here,  indeed meets the criteria for the original circuit to output true. To find a difference answer, the clause
indeed meets the criteria for the original circuit to output true. To find a difference answer, the clause  can be appended and the SAT solver executed again.
can be appended and the SAT solver executed again.
Derivation[edit]
Presented is one possible derivation of the CNF sub-expression for some chosen gates:
AND Gate[edit]
The AND gate is operating properly when the following conditions hold:
- if the output C is true, then one (or both) of its inputs A, B is true
- if the output C is false, then both its inputs A, B are false
express these conditions as an expression that must be satisfied:

convert the implications to AND's and OR's

it's nearly CNF already; complement the rightmost clause twice

apply De Morgan's law once

distribute

apply De Morgan's law

NOT Gate[edit]
The NOT gate is operating properly when its input and output oppose each other. That is:
- if the output C is true, the input A is false
- if the output C is false, the input A is true
express these conditions as an expression that must be satisfied:


NOR Gate[edit]
The NOR gate is operating properly when the following conditions hold:
- if the output C is true, then neither A or B are true
- if the output C is false, then at least one of A and B were true
express these conditions as an expression that must be satisfied:





References[edit]
- G.S. Tseitin: On the complexity of derivation in propositional calculus. In: Slisenko, A.O. (ed.) Structures in Constructive Mathematics and Mathematical Logic, Part II, Seminars in Mathematics (translated from Russian), pp. 115–125. Steklov Mathematical Institute (1968)
 AND
AND
 OR
OR
 NOT
NOT
 XOR
XOR
 NOR
NOR
 NAND
NAND






















































