User:Halibutt/Spacetime/4-vectors

4-vectors and physical law

The first postulate of special relativity declares the equivalency of all inertial frames. A physical law holding in one frame must apply in all frames, since otherwise it would be possible to differentiate between frames. As noted in the previous discussion of energy and momentum conservation, Newtonian momenta fail to behave properly under Lorentzian transformation, and Einstein preferred to change the definition of momentum to one involving 4-vectors rather than give up on conservation of momentum.

Physical laws must be based on constructs that are frame independent. This means that physical laws may take the form of equations connecting scalars, which are always frame independent. However, equations involving 4-vectors require the use of tensors with appropriate rank, which themselves can be thought of as being built up from 4-vectors.

Return to Introduction

Acceleration

Further information: Acceleration (special relativity)

Click here for a brief section summary

It is a common misconception that special relativity is applicable only to inertial frames, and that it is unable to handle accelerating objects or accelerating reference frames. Actually, accelerating objects can generally be analyzed without needing to deal with accelerating frames at all. It is only when gravitation is significant that general relativity is required.

Properly handling accelerating frames does requires some care, however. The difference between special and general relativity is that (1) In special relativity, all velocities are relative, but acceleration is absolute. (2) In general relativity, all motion is relative, whether inertial, accelerating, or rotating. To accommodate this difference, general relativity uses curved spacetime.

In this section, we analyze several scenarios involving accelerated reference frames.

Return to Introduction

Dewan–Beran–Bell spaceship paradox

Main article: Bell's spaceship paradox

The Dewan–Beran–Bell spaceship paradox (Bell's spaceship paradox) is a good example of a problem where intuitive reasoning unassisted by the geometric insight of the spacetime approach can lead to issues.

Figure 4-4. Dewan–Beran–Bell spaceship paradox

In Fig. 4‑4, two identical spaceships float in space and are at rest relative to each other. They are connected by a string which is capable of only a limited amount of stretching before breaking. At a given instant in our frame, the observer frame, both spaceships accelerate in the same direction along the line between them with the same constant proper acceleration. Will the string break?

The main article for this section recounts how, when the paradox was new and relatively unknown, even professional physicists had difficulty working out the solution. Two lines of reasoning lead to opposite conclusions. Both arguments, which are presented below, are flawed even though one of them yields the correct answer.

1. To observers in the rest frame, the spaceships start a distance L apart and remain the same distance apart during acceleration. During acceleration, L is a length contracted distance of the distance L' = γL in the frame of the accelerating spaceships. After a sufficiently long time, γ will increase to a sufficiently large factor that the string must break.
2. Let A and B be the rear and front spaceships. In the frame of the spaceships, each spaceship sees the other spaceship doing the same thing that it is doing. A says that B has the same acceleration that he has, and B sees that A matches her every move. So the spaceships stay the same distance apart, and the string does not break.

The problem with the first argument is that there is no "frame of the spaceships." There cannot be, because the two spaceships measure a growing distance between the two. Because there is no common frame of the spaceships, the length of the string is ill-defined. Nevertheless, the conclusion is correct, and the argument is mostly right. The second argument, however, completely ignores the relativity of simultaneity.

Figure 4-5. The blue lines represent the world lines of two observers A and B who accelerate in the same direction with the same constant magnitude acceleration. At A' and B', the observers stop accelerating. The dotted line is a line of simultaneity for either observer after acceleration stops.

A spacetime diagram (Fig. 4‑5) makes the correct solution to this paradox almost immediately evident. Two observers in Minkowski spacetime accelerate with constant magnitude $k$ acceleration for proper time $\sigma$ (acceleration and elapsed time measured by the observers themselves, not some inertial observer). They are comoving and inertial before and after this phase. In Minkowski geometry, the length of the spacelike line segment $A'B''$ turns out to be greater than the length of the spacelike line segment $AB$.

The length increase can be calculated with the help of the Lorentz transformation. If, as illustrated in Fig. 4‑5, the acceleration is finished, the ships will remain at a constant offset in some frame $S'.$ If $x_{A}$ and $x_{B}=x_{A}+L$ are the ships' positions in $S,$ the positions in frame $S'$ are:

${\begin{aligned}x'_{A}&=\gamma \left(x_{A}-vt\right)\\x'_{B}&=\gamma \left(x_{A}+L-vt\right)\\L'&=x'_{B}-x'_{A}=\gamma L\end{aligned}}$

The "paradox", as it were, comes from the way that Bell constructed his example. In the usual discussion of Lorentz contraction, the rest length is fixed and the moving length shortens as measured in frame $S$. As shown in Fig. 4‑5, Bell's example asserts the moving lengths $AB$ and $A'B'$ measured in frame $S$ to be fixed, thereby forcing the rest frame length $A'B''$ in frame $S'$ to increase.

Return to Introduction

Accelerated observer with horizon

Main articles: Event horizon § Apparent horizon of an accelerated particle, and Rindler coordinates

Certain special relativity problem setups can lead to insight about phenomena normally associated with general relativity, such as event horizons. In the text accompanying Fig. 2‑7, we had noted that the magenta hyperbolae represented actual paths that are tracked by a constantly accelerating traveler in spacetime. During periods of positive acceleration, the traveler's velocity just approaches the speed of light, while, measured in our frame, the traveler's acceleration constantly decreases.

Figure 4-6. Accelerated relativistic observer with horizon. Another well-drawn illustration of the same topic may be viewed here.

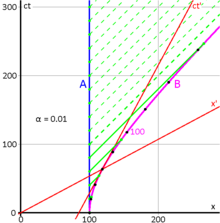
Fig. 4‑6 details various features of the traveler's motions with more specificity. At any given moment, her space axis is formed by a line passing through the origin and her current position on the hyperbola, while her time axis is the tangent to the hyperbola at her position. The velocity parameter $\beta$ approaches a limit of one as $ct$ increases. Likewise, $\gamma$ approaches infinity.

The shape of the invariant hyperbola corresponds to a path of constant proper acceleration. This is demonstrable as follows:

1. We remember that $\beta =ct/x.$
2. Since $c^{2}t^{2}-x^{2}=s^{2},$ we conclude that $\beta (ct)=ct/{\sqrt {c^{2}t^{2}-s^{2}}}.$
3. $\gamma =1/{\sqrt {1-\beta ^{2}}}=$ ${\sqrt {c^{2}t^{2}-s^{2}}}/s$
4. From the relativistic force law, $F=dp/dt=$$dpc/d(ct)=d(\beta \gamma mc^{2})/d(ct).$
5. Substituting $\beta (ct)$ from step 2 and the expression for $\gamma$ from step 3 yields $F=mc^{2}/s,$ which is a constant expression.

Fig. 4‑6 illustrates a specific calculated scenario. Terence (A) and Stella (B) initially stand together 100 light hours from the origin. Stella lifts off at time 0, her spacecraft accelerating at 0.01 c per hour. Every twenty hours, Terence radios updates to Stella about the situation at home (solid green lines). Stella receives these regular transmissions, but the increasing distance (offset in part by time dilation) causes her to receive Terence's communications later and later as measured on her clock, and she never receives any communications from Terence after 100 hours on his clock (dashed green lines).

After 100 hours according to Terence's clock, Stella enters a dark region. She has traveled outside Terence's timelike future. On the other hand, Terence can continue to receive Stella's messages to him indefinitely. He just has to wait long enough. Spacetime has been divided into distinct regions separated by an apparent event horizon. So long as Stella continues to accelerate, she can never know what takes place behind this horizon.

Return to Introduction

Introduction to curved spacetime

Main articles: Introduction to general relativity and General relativity

Basic propositions

Click here for a brief section summary
Note: To avoid navigation issues with the internal wikilinks, mobile phone users should pre-expand all sections from Section Summaries back to the Introduction.

Newton's theories assumed that motion takes place against the backdrop of a rigid Euclidean reference frame that extends throughout all space and all time. Gravity is mediated by a mysterious force, acting instantaneously across a distance, whose actions are independent of the intervening space. In contrast, Einstein denied that there is any background Euclidean reference frame that extends throughout space. Nor is there any such thing as a force of gravitation, only the structure of spacetime itself.

Figure 5-1. Tidal effects

In spacetime terms, the path of a satellite orbiting the Earth is not dictated by the distant influences of the Earth, Moon and Sun. Instead, the satellite moves through space only in response to local conditions. Since spacetime is everywhere locally flat when considered on a sufficiently small scale, the satellite is always following a straight line in its local inertial frame. We say that the satellite always follows along the path of a geodesic. No evidence of gravitation can be discovered following alongside the motions of a single particle.

In any analysis of spacetime, evidence of gravitation requires that one observe the relative accelerations of two bodies or two separated particles. In Fig. 5‑1, two separated particles, free-falling in the gravitational field of the Earth, exhibit tidal accelerations due to local inhomogeneities in the gravitational field such that each particle follows a different path through spacetime. The tidal accelerations that these particles exhibit with respect to each other do not require forces for their explanation. Rather, Einstein described them in terms of the geometry of spacetime, i.e. the curvature of spacetime. These tidal accelerations are strictly local. It is the cumulative total effect of many local manifestations of curvature that result in the appearance of a gravitational force acting at a long range from Earth.

Two central propositions underlie general relativity.

• The first crucial concept is coordinate independence: The laws of physics cannot depend on what coordinate system one uses. This is a major extension of the principle of relativity from the version used in special relativity, which states that the laws of physics must be the same for every observer moving in non-accelerated (inertial) reference frames. In general relativity, to use Einstein's own (translated) words, "the laws of physics must be of such a nature that they apply to systems of reference in any kind of motion." This leads to an immediate issue: In accelerated frames, one feels forces that seemingly would enable one to assess one's state of acceleration in an absolute sense. Einstein resolved this problem through the principle of equivalence.

Figure 5-2. Equivalence principle

• The equivalence principle states that in any sufficiently small region of space, the effects of gravitation are the same as those from acceleration.

In Fig. 5-2, person A is in a spaceship, far from any massive objects, that undergoes a uniform acceleration of g. Person B is in a box resting on Earth. Provided that the spaceship is sufficiently small so that tidal effects are non-measurable (given the sensitivity of current gravity measurement instrumentation, A and B presumably should be Lilliputians), there are no experiments that A and B can perform which will enable them to tell which setting they are in.

An alternative expression of the equivalence principle is to note that in Newton's universal law of gravitation, F = GMm_g /r² = m_gg and in Newton's second law, F = m_ia, there is no a priori reason why the gravitational mass m_g should be equal to the inertial mass m_i. The equivalence principle states that these two masses are identical.

To go from the elementary description above of curved spacetime to a complete description of gravitation requires tensor calculus and differential geometry, topics both requiring considerable study. Without these mathematical tools, it is possible to write about general relativity, but it is not possible to demonstrate any non-trivial derivations.

Rather than this section attempting to offer a (yet another) relatively non-mathematical presentation about general relativity, the reader is referred to the featured Wikipedia articles Introduction to general relativity and General relativity.

Instead, the focus in this section will be to explore a handful of elementary scenarios that serve to give somewhat of the flavor of general relativity.

Return to Introduction