User:HerrHartmuth/sandbox
Similarity to symmetric tridiagonal matrix[edit]
Given a given real tridiagonal, unsymmetic matrix
where .
Assume that the product of off-diagonal entries is strictly positive and define a transformation matrix by
The similarity transformation yields a symmetric tridiagonal matrix by
Note that and have the same eigenvalues.
Special Case: Real Tridiagonal[edit]
In the case of a tridiagonal structure with real elements the eigenvalues and eigenvectors can be derived explicity as
Legendre[edit]
Pointwise Evaluations[edit]
As shown before the values at the boundary are given by
One can show that for the values are given by
Carrier Gen + Recomb[edit]
Radiative recombination[edit]
During radiative recombination, a form of spontaneous emission, a photon is emitted with the wavelength corresponding to the energy released. This effect is the basis of LEDs. Because the photon carries relatively little momentum, radiative recombination is significant only in direct bandgap materials.
When photons are present in the material, they can either be absorbed, generating a pair of free carriers, or they can stimulate a recombination event, resulting in a generated photon with similar properties to the one responsible for the event. Absorption is the active process in photodiodes, solar cells, and other semiconductor photodetectors, while stimulated emission is responsible for laser action in laser diodes.
In thermal equilibrium the radiative recombination and thermal generation rate equal each other[1]
where is called the radiative capture probability and the intrinsic carrier density.
Under steady-state conditions the radiative recombination rate and resulting net recombination rate are[2]
where the carrier densities are made up of equilibrium and excess densities
The radiative lifetime is given by[3]
Auger recombination[edit]
In Auger recombination the energy is given to a third carrier, which is excited to a higher energy level without moving to another energy band. After the interaction, the third carrier normally loses its excess energy to thermal vibrations. Since this process is a three-particle interaction, it is normally only significant in non-equilibrium conditions when the carrier density is very high. The Auger effect process is not easily produced, because the third particle would have to begin the process in the unstable high-energy state.
The Auger recombination can be calculated from the equation[clarification needed] :
In thermal equilibrium the Auger recombination and thermal generation rate equal each other[4]
where are the Auger capture probabilities.
The non-equilibrium Auger recombination rate and resulting net recombination rate under steady-state conditions are[5]
The Auger lifetime is given by[6]
Auger recombination in LEDs[edit]
The mechanism causing LED efficiency droop was identified in 2007 as Auger recombination, which met with a mixed reaction.[7] In 2013, an experimental study claimed to have identified Auger recombination as the cause of efficiency droop.[8] However, it remains disputed whether the amount of Auger loss found in this study is sufficient to explain the droop. Other frequently quoted evidence against Auger as the main droop causing mechanism is the low-temperature dependence of this mechanism which is opposite to that found for the drop.
MINRES[edit]
In mathematics, the minimal residual method (MINRES) is an iterative method for the numerical solution of a symmetric but possibly indefinite system of linear equations. The method approximates the solution by the vector in a Krylov subspace with minimal residual. The Lanczos algorithm is used to find this vector.
Introduction[edit]
One tries to solve the following square system of linear equations
where is unknown and are given.
In the special case of being symmetric and positive-definite one can use the Conjugate gradient method. For symmetric and possibly indefinite matrices one uses the MINRES method. In the case of unsymmetric and indefinite matrices one needs to fall back to methods such as the GMRES, or Bi-CG.
The method[edit]
Krylov space basis[edit]
The matrix is symmetric and thus one can apply the Lanczos method to find an orthogonal basis for the Krylov subspace
Denote the Euclidean norm of any vector v by . Denote the (square) system of linear equations to be solved by
The matrix A is assumed to be invertible of size m-by-m. Furthermore, it is assumed that b is normalized, i.e., that .
The n-th Krylov subspace for this problem is
GMRES approximates the exact solution of by the vector that minimizes the Euclidean norm of the residual .
The vectors might be close to linearly dependent, so instead of this basis, the Arnoldi iteration is used to find orthonormal vectors which form a basis for . Hence, the vector can be written as with , where is the m-by-n matrix formed by .
The Arnoldi process also produces an ()-by- upper Hessenberg matrix with
Because columns of are orthogonal, we have
where
is the first vector in the standard basis of , and
being the first trial vector (usually zero). Hence, can be found by minimizing the Euclidean norm of the residual
This is a linear least squares problem of size n.
This yields the GMRES method. On the -th iteration:
- calculate with the Arnoldi method;
- find the which minimizes ;
- compute ;
- repeat if the residual is not yet small enough.
At every iteration, a matrix-vector product must be computed. This costs about floating-point operations for general dense matrices of size , but the cost can decrease to for sparse matrices. In addition to the matrix-vector product, floating-point operations must be computed at the n -th iteration.
Convergence[edit]
The nth iterate minimizes the residual in the Krylov subspace Kn. Since every subspace is contained in the next subspace, the residual does not increase. After m iterations, where m is the size of the matrix A, the Krylov space Km is the whole of Rm and hence the GMRES method arrives at the exact solution. However, the idea is that after a small number of iterations (relative to m), the vector xn is already a good approximation to the exact solution.
This does not happen in general. Indeed, a theorem of Greenbaum, Pták and Strakoš states that for every nonincreasing sequence a1, …, am−1, am = 0, one can find a matrix A such that the ||rn|| = an for all n, where rn is the residual defined above. In particular, it is possible to find a matrix for which the residual stays constant for m − 1 iterations, and only drops to zero at the last iteration.
In practice, though, GMRES often performs well. This can be proven in specific situations. If the symmetric part of A, that is , is positive definite, then
where and denote the smallest and largest eigenvalue of the matrix , respectively.[9]
If A is symmetric and positive definite, then we even have
where denotes the condition number of A in the Euclidean norm.
In the general case, where A is not positive definite, we have
where Pn denotes the set of polynomials of degree at most n with p(0) = 1, V is the matrix appearing in the spectral decomposition of A, and σ(A) is the spectrum of A. Roughly speaking, this says that fast convergence occurs when the eigenvalues of A are clustered away from the origin and A is not too far from normality.[10]
All these inequalities bound only the residuals instead of the actual error, that is, the distance between the current iterate xn and the exact solution.
Extensions of the method[edit]
Like other iterative methods, GMRES is usually combined with a preconditioning method in order to speed up convergence.
The cost of the iterations grow as O(n2), where n is the iteration number. Therefore, the method is sometimes restarted after a number, say k, of iterations, with xk as initial guess. The resulting method is called GMRES(k) or Restarted GMRES. This methods suffers from stagnation in convergence as the restarted subspace is often close to the earlier subspace.
The shortcomings of GMRES and restarted GMRES are addressed by the recycling of Krylov subspace in the GCRO type methods such as GCROT and GCRODR.[11] Recycling of Krylov subspaces in GMRES can also speed up convergence when sequences of linear systems need to be solved.[12]
Comparison with other solvers[edit]
The Arnoldi iteration reduces to the Lanczos iteration for symmetric matrices. The corresponding Krylov subspace method is the minimal residual method (MinRes) of Paige and Saunders. Unlike the unsymmetric case, the MinRes method is given by a three-term recurrence relation. It can be shown that there is no Krylov subspace method for general matrices, which is given by a short recurrence relation and yet minimizes the norms of the residuals, as GMRES does.
Another class of methods builds on the unsymmetric Lanczos iteration, in particular the BiCG method. These use a three-term recurrence relation, but they do not attain the minimum residual, and hence the residual does not decrease monotonically for these methods. Convergence is not even guaranteed.
The third class is formed by methods like CGS and BiCGSTAB. These also work with a three-term recurrence relation (hence, without optimality) and they can even terminate prematurely without achieving convergence. The idea behind these methods is to choose the generating polynomials of the iteration sequence suitably.
None of these three classes is the best for all matrices; there are always examples in which one class outperforms the other. Therefore, multiple solvers are tried in practice to see which one is the best for a given problem.
Solving the least squares problem[edit]
One part of the GMRES method is to find the vector which minimizes
Note that is an (n + 1)-by-n matrix, hence it gives an over-constrained linear system of n+1 equations for n unknowns.
The minimum can be computed using a QR decomposition: find an (n + 1)-by-(n + 1) orthogonal matrix Ωn and an (n + 1)-by-n upper triangular matrix such that
The triangular matrix has one more row than it has columns, so its bottom row consists of zero. Hence, it can be decomposed as
where is an n-by-n (thus square) triangular matrix.
The QR decomposition can be updated cheaply from one iteration to the next, because the Hessenberg matrices differ only by a row of zeros and a column:
where hn+1 = (h1,n+1, …, hn+1,n+1)T. This implies that premultiplying the Hessenberg matrix with Ωn, augmented with zeroes and a row with multiplicative identity, yields almost a triangular matrix:
This would be triangular if σ is zero. To remedy this, one needs the Givens rotation
where
With this Givens rotation, we form
Indeed,
is a triangular matrix.
Given the QR decomposition, the minimization problem is easily solved by noting that
Denoting the vector by
with gn ∈ Rn and γn ∈ R, this is
The vector y that minimizes this expression is given by
Again, the vectors are easy to update.[13]
Example code[edit]
Regular GMRES (MATLAB / GNU Octave)[edit]
function [x, e] = gmres( A, b, x, max_iterations, threshold)
n = length(A);
m = max_iterations;
%use x as the initial vector
r=b-A*x;
b_norm = norm(b);
error = norm(r)/b_norm;
%initialize the 1D vectors
sn = zeros(m,1);
cs = zeros(m,1);
e1 = zeros(n,1);
e1(1) = 1;
e=[error];
r_norm=norm(r);
Q(:,1) = r/r_norm;
beta = r_norm*e1;
for k = 1:m
%run arnoldi
[H(1:k+1,k) Q(:,k+1)] = arnoldi(A, Q, k);
%eliminate the last element in H ith row and update the rotation matrix
[H(1:k+1,k) cs(k) sn(k)] = apply_givens_rotation(H(1:k+1,k), cs, sn, k);
%update the residual vector
beta(k+1) = -sn(k)*beta(k);
beta(k) = cs(k)*beta(k);
error = abs(beta(k+1)) / b_norm;
%save the error
e=[e; error];
if ( error <= threshold)
break;
end
end
%calculate the result
y = H(1:k,1:k) \ beta(1:k);
x = x + Q(:,1:k)*y;
end
%----------------------------------------------------%
% Arnoldi Function %
%----------------------------------------------------%
function [h, q] = arnoldi(A, Q, k)
q = A*Q(:,k);
for i = 1:k
h(i)= q'*Q(:,i);
q = q - h(i)*Q(:,i);
end
h(k+1) = norm(q);
q = q / h(k+1);
end
%---------------------------------------------------------------------%
% Applying Givens Rotation to H col %
%---------------------------------------------------------------------%
function [h, cs_k, sn_k] = apply_givens_rotation(h, cs, sn, k)
%apply for ith column
for i = 1:k-1
temp = cs(i)*h(i) + sn(i)*h(i+1);
h(i+1) = -sn(i)*h(i) + cs(i)*h(i+1);
h(i) = temp;
end
%update the next sin cos values for rotation
[cs_k sn_k] = givens_rotation(h(k), h(k+1));
%eliminate H(i+1,i)
h(k) = cs_k*h(k) + sn_k*h(k+1);
h(k+1) = 0.0;
end
%%----Calculate the Given rotation matrix----%%
function [cs, sn] = givens_rotation(v1, v2)
if (v1==0)
cs = 0;
sn = 1;
else
t=sqrt(v1^2+v2^2);
cs = abs(v1) / t;
sn = cs * v2 / v1;
end
end
See also[edit]
References[edit]
- ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 140. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 140. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 140. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 143. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 143. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Li, Sheng S., ed. (2006). "Semiconductor Physical Electronics": 144. doi:10.1007/0-387-37766-2.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Stevenson, Richard (August 2009) The LED’s Dark Secret: Solid-state lighting won't supplant the lightbulb until it can overcome the mysterious malady known as droop. IEEE Spectrum
- ^ Justin Iveland; Lucio Martinelli; Jacques Peretti; James S. Speck; Claude Weisbuch. "Cause of LED Efficiency Droop Finally Revealed". Physical Review Letters, 2013. Science Daily. Retrieved 23 April 2013.
- ^ Eisenstat, Elman & Schultz, Thm 3.3. NB all results for GCR also hold for GMRES, cf. Saad & Schultz
- ^ Trefethen & Bau, Thm 35.2
- ^ Amritkar, Amit; de Sturler, Eric; Świrydowicz, Katarzyna; Tafti, Danesh; Ahuja, Kapil (2015). "Recycling Krylov subspaces for CFD applications and a new hybrid recycling solver". Journal of Computational Physics. 303: 222. doi:10.1016/j.jcp.2015.09.040.
- ^ Gaul, André (2014). Recycling Krylov subspace methods for sequences of linear systems (Ph.D.). TU Berlin. doi:10.14279/depositonce-4147.
- ^ Stoer and Bulirsch, §8.7.2
Notes[edit]
- A. Meister, Numerik linearer Gleichungssysteme, 2nd edition, Vieweg 2005, ISBN 978-3-528-13135-7.
- Y. Saad, Iterative Methods for Sparse Linear Systems, 2nd edition, Society for Industrial and Applied Mathematics, 2003. ISBN 978-0-89871-534-7.
- Y. Saad and M.H. Schultz, "GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems", SIAM J. Sci. Stat. Comput., 7:856–869, 1986. doi:10.1137/0907058.
- S. C. Eisenstat, H.C. Elman and M.H. Schultz, "Variational iterative methods for nonsymmetric systems of linear equations", SIAM Journal on Numerical Analysis, 20(2), 345–357, 1983.
- J. Stoer and R. Bulirsch, Introduction to numerical analysis, 3rd edition, Springer, New York, 2002. ISBN 978-0-387-95452-3.
- Lloyd N. Trefethen and David Bau, III, Numerical Linear Algebra, Society for Industrial and Applied Mathematics, 1997. ISBN 978-0-89871-361-9.
- Dongarra et al. , Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd Edition, SIAM, Philadelphia, 1994
- Amritkar, Amit; de Sturler, Eric; Świrydowicz, Katarzyna; Tafti, Danesh; Ahuja, Kapil (2015). "Recycling Krylov subspaces for CFD applications and a new hybrid recycling solver". Journal of Computational Physics 303: 222. doi:10.1016/j.jcp.2015.09.040
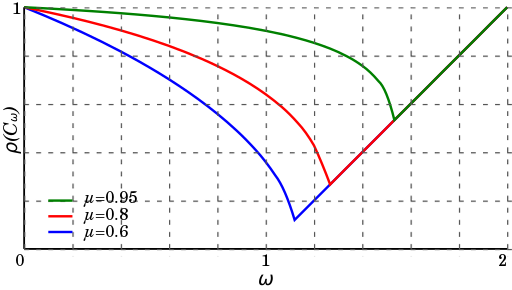
SOR - Convergence Rate[edit]
Convergence[edit]
The choice of relaxation factor ω is not necessarily easy, and depends upon the properties of the coefficient matrix. In 1947, Ostrowski proved that if is symmetric and positive-definite then for . Thus, convergence of the iteration process follows, but we are generally interested in faster convergence rather than just convergence.
Convergence Rate[edit]
The convergence rate for the SOR method can be analytically derived. One needs to assume the following
- the relaxation parameter is appropriate:
- Jacobi's iteration matrix has only real eigenvalues
- Jacobi's method is convergent:
- a unique solution exists: .
Then the convergence rate can be expressed as[1]
where the optimal relaxation parameter is given by
ILU - Stability[edit]
Concerning the stability of the ILU the following theorem was proven by Meijerink an van der Vorst[2].
Let be an M-matrix, the (complete) LU decomposition given by , and the ILU by . Then
holds. Thus, the ILU is at least as stable as the (complete) LU decomposition.
ILU - Definition[edit]
For a given matrix one defines the graph as
which is used to define the conditions a sparsity patterns needs to fulfill
A decomposition of the form which fulfills
- is a lower unitriangular matrix
- is an upper triangular matrix
- are zero outside of the sparsity pattern:
- is zero within the sparsity pattern:
is called an incomplete LU decomposition (w.r.t. the sparsity pattern ).
The sparsity pattern of L and U is often chosen to be the same as the sparsity pattern of the original matrix A. If the underlying matrix structure can be referenced by pointers instead of copied, the only extra memory required is for the entries of L and U. This preconditioner is called ILU(0).
CG - Convergence Theorem[edit]
Define a subset of polynomials as
where is the set of polynomials of maximal degree .
Let be the iterative approximations of the exact solution , and define the errors as . Now, the rate of convergence can be approximated as [3]
where denotes the spectrum, and denotes the condition number.
Note, the important limit when tends to
This limit shows a faster convergence rate compared to the iterative methods of Jacobi or Gauss-Seidel which scale as .
SOR - Symmetric positive definite case[edit]
In case that the system matrix is of positive definite type one can show convergence.
Let be the iteration matrix. Then, convergence is guarenteed for
Jacobi - Symmetric positive definite case[edit]
In case that the system matrix is of positive definite type one can show convergence.
Let be the iteration matrix. Then, convergence is guarenteed for
where is the maximal eigenvalue.
The spectral radius can be minimized for a particular choice of as follows
where is the matrix' condition number.
Hyperbolic system of partial differential equations[edit]
The following is a system of first order partial differential equations for unknown functions , , where :
where are once continuously differentiable functions, nonlinear in general.
Next, for each a Jacobian matrix is defined
The system is hyperbolic if for all the matrix has only real eigenvalues and is diagonalizable.
If the matrix has s distinct real eigenvalues, it follows that it is diagonalizable. In this case the system is called strictly hyperbolic.
If the matrix is symmetric, it follows that it is diagonalizable and the eigenvalues are real. In this case the system is called symmetric hyperbolic.
Linear system[edit]
The case of a linear hyperbolic system of conservation laws (with constant coefficients in one space dimension) is given by
where one solves for the unknown function and initial data , and are given.
A hyperbolic system is real diagonalizable
Thus, the conservation law decouples into independent transport equations
The general solution is
and in the original variables for given initial data
Example: The Laplace operator[edit]
The (continuous) Laplace operator in -dimensions is given by . The discrete Laplace operator depends on the dimension .
In 1D the Laplace operator is approximated as
This approximation is usually expressed via the following stencil
The 2D case shows all the characteristics of the more general nD case. Each second partial derivative needs to be approximated similar to the 1D case
which is usually given by the following stencil
Consistency[edit]
Consistency of the above mentioned approximation can be shown for highly regular functions, such as . The statement is
To proof this one needs to substitute Taylor Series expansions up to order 3 into the discrete Laplace operator.
Properties[edit]
Subharmonic[edit]
Similar to continous subharmonic functions one can define subharmonic functions for finite-difference approximations
Mean value[edit]
One can define a general stencil of positive type via
If is (discrete) subharmonic, then the following mean value property holds
where the approximation is evaluated on points of the grid, and the stencil is assumed to be of positive type.
A similar mean value property also holds for the continuous case.
Maximum principle[edit]
For a (discrete) subharmonic function the following holds
where are discretizations of the continuous domain , respectively the boundary .
Discontinuous Galerkin Scheme[edit]
Scalar hyperbolic conservation law[edit]
A scalar hyperbolic conservation law is of the form
where one tries to solve for the unknown scalar function , and the functions are typically given.
Space discretization[edit]
The -space will be discretized as
Furthermore, we need the following definitions
Basis for function space[edit]
We derive the basis representation for the function space of our solution . The function space is defined as
where denotes the restriction of onto the interval , and denotes the space of polynomials of maximal degree . The index should show the relation to an underlying discretization given by . Note here that is not uniquely defined at the intersection points .
At first we make use of a specific polynomial basis on the interval , the Legendre_polynomials , i.e.,
Note especially the orthogonality relations
Transformation onto the interval , and normalization is achieved by functions
which fulfill the orthonormality relation
Transformation onto an interval is given by
which fulfill
For -normalization we define , and for -normalization we define , s.t.
Finally, we can define the basis representation of our solutions
Note here, that is not defined at the interface positions.
DG-Scheme[edit]
The conservation law is transformed into its weak form by multiplying with test functions, and integration over test intervals
By using partial integration one is left with
The fluxes at the interfaces are approximated by numerical fluxes with
where denotes the left- and right-hand sided limits. Finally, the DG-Scheme can be written as
- ^ Hackbusch, Wolfgang. "4.6.2". Iterative Solution of Large Sparse Systems of Equations | SpringerLink. doi:10.1007/978-3-319-28483-5.
- ^ Meijerink, J. A.; Vorst, Van Der; A, H. (1977). "An iterative solution method for linear systems of which the coefficient matrix is a symmetric 𝑀-matrix". Mathematics of Computation. 31 (137): 148–162. doi:10.1090/S0025-5718-1977-0438681-4. ISSN 0025-5718.
- ^ 1948-, Hackbusch, W.,. Iterative solution of large sparse systems of equations (Second edition ed.). Switzerland. ISBN 9783319284835. OCLC 952572240.
{{cite book}}:|edition=has extra text (help);|last=has numeric name (help)CS1 maint: extra punctuation (link) CS1 maint: multiple names: authors list (link)






































































































































































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle \left\langle P_{i},P_{j}\right\rangle _{L^{2}([-1,1])}={\frac {2}{2i+1}}\delta _{ij}\quad \forall \,i,j\in \mathbb {N} _{0}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/047ab4c461c39325d103b96d60634fe690fef639)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

![{\displaystyle \phi _{i}(x):={\sqrt {2i+1}}P_{i}(2x-1)\quad {\text{for}}\quad x\in [0,1]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/368199c3f0b58380c1956153a314ded343f1dd69)
![{\displaystyle \left\langle \phi _{i},\phi _{j}\right\rangle _{L^{2}([0,1])}=\delta _{ij}\quad \forall \,i,j\in \mathbb {N} _{0}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ec177dd2b386bd8414c869a0c5777d94b66b46)







![{\displaystyle \|\varphi _{ki}\|_{L^{\infty }(I_{k})}=\|\phi _{i}\|_{L^{\infty }([0,1])}=:c_{i,\infty }\quad {\text{and}}\quad \|{\tilde {\varphi }}_{ki}\|_{L^{1}(I_{k})}=\|\phi _{i}\|_{L^{1}([0,1])}=:c_{i,1}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9d377173d2f2842da2bc6eaaedfd70730109f8c)






