User:Incredio/Drafts
for Langley Extrapolation[edit]



for use in pipeline[edit]
Langeled . With the energy content of natural gas at 39 MJ (megajoules) per normal cubic meter, gives an energy flux of 31.5 GW.
for possible use in Milankovitch Cycles?[edit]

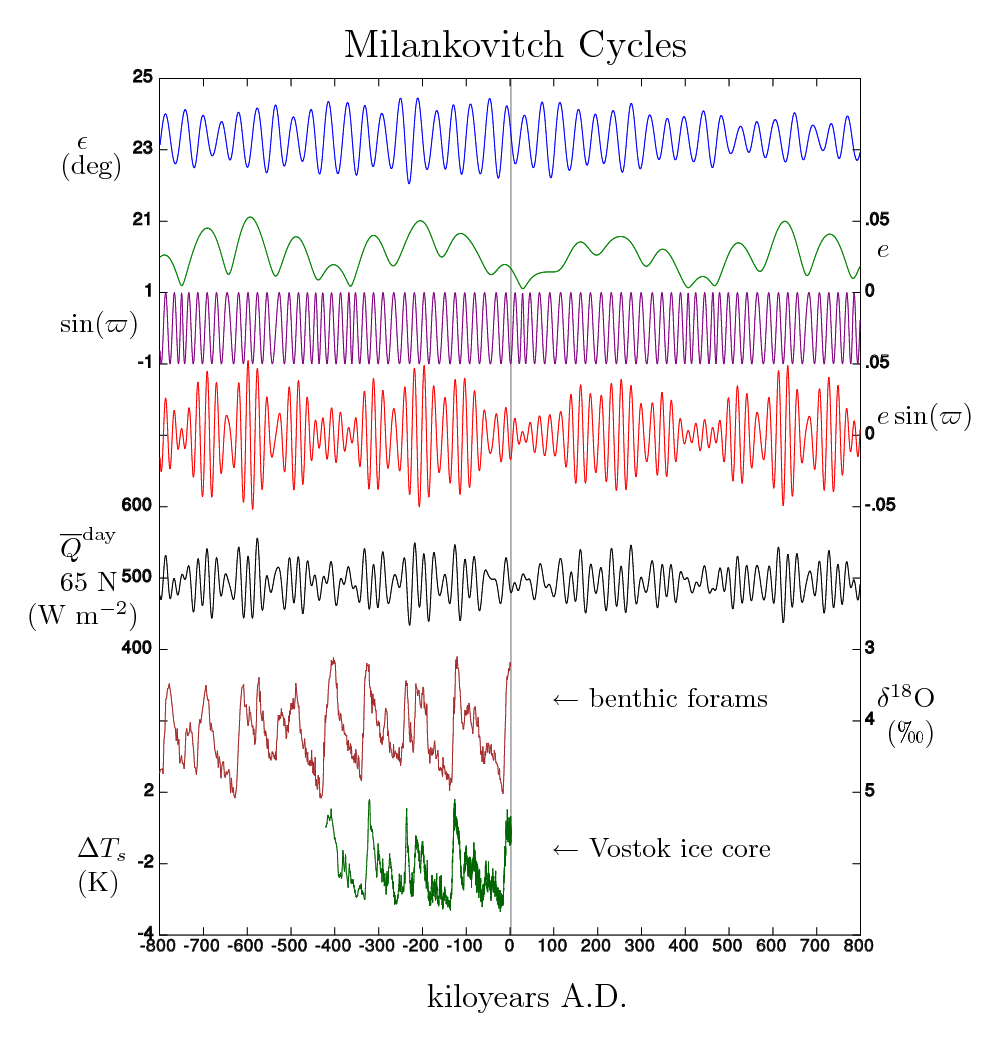
These figures are for the purpose of emphasizing future Milankovitch_cycles. The long time series highlights the rarity of the low-eccentricity regime that we have entered. Since the current reduced NH summer insolation was not sufficient to trigger a glaciation, we may need to wait to 60,000 AD, 130,000 AD or 622,000 AD to reach a sufficient trigger. See No soon Ice Age, says astronomy for original advocacy of this claim.
symbol for longitude of perihelion[edit]
See the symbol in Britannica
and at Swinburne: "A related quantity is the longitude of perihelion, ϖ, although the distinction between these two quantities is often blurred."
and in this doc, where the LaTeX symbol is \varpi, . Here is how to do it in html: ϖ ϖ
draft revision for Apsis[edit]
For the Earth's orbit around the sun, the time of apsis is most relevantly expressed in terms of a time relative to seasons, for that will determine the contribution of the elliptic orbit to seasonal forcing, meaning the annual variation in insolation at the top of the atmosphere. This forcing is primarily controlled by the annual cycle of the declination of the sun, a consequence of the tilt of the Earth's rotation axis relative to the plane of the orbit. Currently, perihelion occurs about 14 days after the winter solstice, making northern hemisphere winters milder than they would be otherwise, and southern hemisphere winters more extreme. The time of perihelion progresses through the seasons, making one complete cycle in 22,000 to 26,000 years, a contribution to Milankovitch cycles, a forcing of the ice ages, known as precession.
A common convention is to express the timing of perihelion relative to the vernal equinox not in days, but as an angle of orbital displacement, a longitude of the periapsis. For Earth's orbit, this would be a longitude of perihelion.
distribution of insolation at the top of the atmosphere[edit]


The theory for the distribution of solar radiation at the top of the atmosphere concerns how the solar irradiance (the power of solar radiation per unit area) at the top of the atmosphere is determined by the sphericity and orbital parameters of Earth. The theory could be applied to any monodirectional beam of radiation incident onto a rotating sphere, but is most usually applied to sunlight, and in particular for application in numerical weather prediction, and theory for the seasons and the ice ages. The last application is known as Milankovitch cycles.
The derivation of distribution is based on a fundamental identity from spherical trigonometry, the spherical law of cosines:
where a, b and c are arc lengths, in radians, of the sides of a spherical triangle. C is the angle in the vertex opposite the side which has arc length c. Applied to the calculation of solar zenith angle Θ, we equate the following for use in the spherical law of cosines:
The distance of Earth from the sun can be denoted RE, and the mean distance can be denoted R0, which is very close to 1 AU. The insolation onto a plane normal to the solar radiation, at a distance 1 AU from the sun, is the solar constant, denoted S0. The solar flux density (insolation) onto a plane tangent to the sphere of the Earth, but above the bulk of the atmosphere (elevation 100 km or greater) is:
and
The average of Q over a day is the average of Q over one rotation, or the hour angle progressing from h=π to h=-π:
Let h0 be the hour angle when Q becomes positive. This could occur at
sunrise when , or for h0 as a solution of
or
If tan(φ)tan(δ)>1, then the sun does not set and the sun is already risen at h=π, so ho=π. If tan(φ)tan(δ)<-1, the sun does not rise and .
is nearly constant over the course of a day, and can be taken outside the integral
Let θ be the conventional polar angle describing a planetary orbit. For convenience, let θ=0 at the vernal equinox. The declination δ as a function of orbital position is
where ε is the obliquity. The conventional longitude of perihelion ϖ is defined relative to the vernal equinox, so for the elliptical orbit:
or
With knowledge of ϖ, ε and e from astrodynamical calculations [1] and So from a consensus of observations or theory, can be calculated for any latitude φ and θ. Note that because of the elliptical orbit, and as a simple consequence of Kepler's second law, θ does not progress exactly uniformly with time. Nevertheless, θ=0° is exactly the time of the vernal equinox, θ=90° is exactly the time of the summer solstice, θ=180° is exactly the time of the autumnal equinox and θ=270° is exactly the time of the winter solstice.
application to Milankovitch cycles[edit]
Obtaining a time series for a for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is simply equal to the obliquity ε. The distance from the sun is

For this summer solstice calculation, the role of the elliptical orbit is entirely contained within the important product , which is known as the precession index, the variation of which dominates the variations in insolation at 65 N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity will be dominant.
for Radiative Forcing[edit]
still images were more effective:























![{\displaystyle \int _{h=\pi }^{h=-\pi }Qdh=S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h)\right]_{h=h_{o}}^{h=-h_{o}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeac37a65f42dc70a067dcc1efd936351132994b)
![{\displaystyle \int _{h=\pi }^{h=-\pi }Qdh=-2S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0598984f8951d56cbf40d1d0746488a51de19e1c)
![{\displaystyle {\overline {Q}}^{\mathrm {day} }={\frac {S_{o}}{\pi }}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59eec325bea63644af8668d48d9624a08b1949f9)




