User:User A1/sandbox/Bernoulli's principle
- Bernoulli's equation redirects here; see Bernoulli differential equation for an unrelated topic in ordinary differential equations.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (september 2007) |
Bernoulli's Principle states that for an ideal fluid (low speed air is a good approximation), with no work being performed on the fluid, an increase in velocity occurs simultaneously with decrease in pressure or a change in the fluid's gravitational potential energy.
This principle is a simplification of Bernoulli's equation, which states that the sum of all forms of energy in a fluid flowing along an enclosed path (a streamline) is the same at any two points in that path.
Incompressible flow[edit]
Liquids are so dense they can be considered to be of constant density, regardless of their pressure. For this reason liquids can be considered to be incompressible and the flow of liquids can be described as incompressible flow. Bernoulli performed his experiments on liquids and his equation is valid only for incompressible flow. Bernoulli's equation is also valid for the flow of gases providing the velocity of the gas is sufficiently low that the variation in density of the gas along each streamline can be ignored.
The original form of Bernoulli's equation is:
where:
- v = fluid velocity at a point on a streamline
- g = acceleration due to gravity
- h = height of the point on the streamline
- p = pressure at the point on the streamline
- = density of the fluid at all points on the streamline
This can be rewritten as[1]:
where:
- q = dynamic pressure
These assumptions must be met for the equation to apply:
- The equation applies along a streamline.
- The fluid in incompressible to keep a constant density
- For constant-density fluids potential flow, it applies throughout the entire flow field.
An increase in velocity and the corresponding decrease in pressure, as shown by the equation, is often called Bernoulli's principle.
Bernoulli's equation can be used to calculate lift in cases where its assumptions are not violated.
The above equations clearly use a linear relationship between velocity squared and pressure. For real fluids such as water and air this relationship is only linear for low speeds. The equation suggests there is a velocity at which pressure is zero; and at higher velocities the pressure is negative! Gases and liquids are not capable of negative pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid long before zero pressure is reached.
Compressible flow[edit]
A second, more general form of Bernoulli's equation may be written for compressible fluids, in which case, following a streamline:
- = gravitational potential energy per unit mass, in the case of a uniform gravitational field
- = fluid enthalpy per unit mass, which is also often written as (which conflicts with the use of in this article for "height"). Note that where is the fluid thermodynamic energy per unit mass, also known as the specific internal energy or "sie".
The constant on the right hand side is often called the Bernoulli constant and denoted . For steady inviscid adiabatic flow with no additional sources or sinks of energy, is constant along any given streamline. More generally, when may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).
When shock waves are present, in a reference frame moving with a shock, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter itself, however, remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.
Derivations of Bernoulli equation[edit]
Incompressible fluids[edit]
The Bernoulli equation for incompressible fluids can be derived by integrating the Euler equations, or applying the law of conservation of energy in two sections along a streamline, ignoring viscosity, compressibility, and thermal effects.
The simplest derivation is to first ignore gravity and consider constrictions and expansions in pipes that are otherwise straight, as seen in Venturi effect. Let the x axis be directed down the axis of the pipe.
The equation of motion for a parcel of fluid on the axis of the pipe is
In steady flow, so
With constant, the equation of motion can be written as
or
where is a constant, sometimes referred to as the Bernoulli constant. It is not a universal constant, but rather a constant of a particular fluid system. We deduce that where the speed is large, pressure is low and vice versa. In the above derivation, no external work-energy principle is invoked. Rather, the work-energy principle was inherently derived by a simple manipulation of the momentum equation.
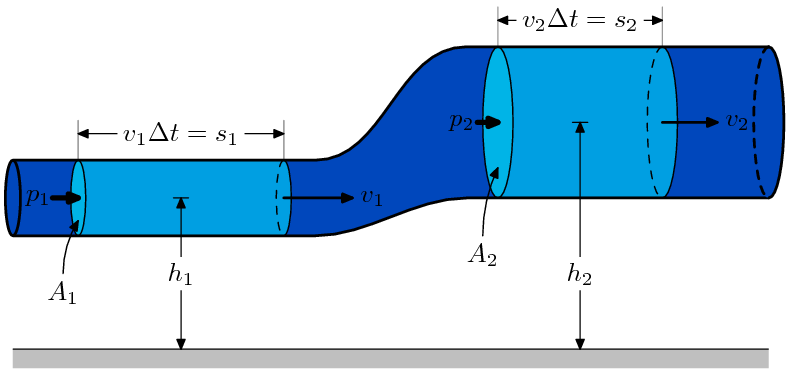
Applying conservation of energy in form of the work-kinetic energy theorem we find that:
- the change in KE of the system equals the net work done on the system;
Therefore,
- the work done by the forces in the fluid + decrease in potential energy = increase in kinetic energy.
The work done by the forces is
The decrease of potential energy is
The increase in kinetic energy is
Putting these together,
or
After dividing by , and (= rate of fluid flow = as the fluid is incompressible):
or, as stated in the first paragraph:
- (Eqn. 1)
Further division by g produces the following equation. Note that each term can be described in the length dimension (such as meters). This is the head equation derived from Bernoulli's Principle:
- (Eqn. 2a)
The middle term, h, can be called an elevation head, although height is used throughout this discussion. represents the internal energy of the fluid due to its height above a reference plane.
A free falling mass from a height h (in a vacuum) will reach a velocity
- or when we rearrange it as a head:
The term is called the velocity head, expressed as a length measurement. It represents the internal energy of the fluid due to its motion.
The hydrostatic pressure p is defined as
- , or when we rearrange it as a head:
The term is also called the pressure head, expressed as a length measurement. It represents the internal energy of the fluid due to the pressure exerted on the container.
When we combine the head due to the velocity and the head due to static pressure with the elevation above a reference point, we obtain a simple relationship useful for incompressible fluids.
- (Eqn. 2b)
If we were to multiply Eqn. 1 by the density of the fluid, we would get an equation with three pressure terms:
- (Eqn. 3)
We note that the pressure of the system is constant in this form of the Bernoulli Equation. If the static pressure of the system (the far right term) increases, and if the pressure due to elevation (the middle term) is constant, then we know that the dynamic pressure (the left term) must have decreased. In other words, if the speed of a fluid decreases and it is not due to an elevation difference, we know it must be due to an increase in the static pressure that is resisting the flow.
All three equations are merely simplified versions of an energy balance on a system.
Compressible fluids[edit]
The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of time , the amount of mass passing through the boundary defined by the area is equal to the amount of mass passing outwards through the boundary defined by the area :
- .
Conservation of energy is applied in a similar manner: It is assumed that the change in energy of the volume of the streamtube bounded by and is due entirely to energy entering or leaving through one or the other of these two boundaries. Clearly, in a more complicated situation such as a fluid flow coupled with radiation, such conditions are not met. Nevertheless, assuming this to be the case and assuming the flow is steady so that the net change in the energy is zero,
where and are the energy entering through and leaving through , respectively.
The energy entering through is the sum of the kinetic energy entering, the energy entering in the form of potential gravitational energy of the fluid, the fluid thermodynamic energy entering, and the energy entering in the form of mechanical work:
A similar expression for may easily be constructed. So now setting :
which can be rewritten as:
Now, using the previously-obtained result from conservation of mass, this may be simplified to obtain
which is the Bernoulli equation for compressible flow.
See also[edit]
- Navier-Stokes equations - The Navier-Stokes equations for fluid flow
- Euler equations - A special case of the Navier-Stokes equation for an inviscid fluid
















































![{\displaystyle \Delta E_{1}=\left[{\frac {1}{2}}\rho _{1}v_{1}^{2}+\phi _{1}\rho _{1}+\epsilon _{1}\rho _{1}+p_{1}\right]A_{1}v_{1}\,\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59e891fa421f29ad49f08dbd9fe97e2d9bd7e10)

![{\displaystyle 0=\left[{\frac {1}{2}}\rho _{1}v_{1}^{2}+\phi _{1}\rho _{1}+\epsilon _{1}\rho _{1}+p_{1}\right]A_{1}v_{1}\,\Delta t-\left[{\frac {1}{2}}\rho _{2}v_{2}^{2}+\phi _{2}\rho _{2}+\epsilon _{2}\rho _{2}+p_{2}\right]A_{2}v_{2}\,\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a6110cfed41eea227fb5896885a1deed623cf56)
![{\displaystyle 0=\left[{\frac {1}{2}}v_{1}^{2}+\phi _{1}+\epsilon _{1}+{\frac {p_{1}}{\rho _{1}}}\right]\rho _{1}A_{1}v_{1}\,\Delta t-\left[{\frac {1}{2}}v_{2}^{2}+\phi _{2}+\epsilon _{2}+{\frac {p_{2}}{\rho _{2}}}\right]\rho _{2}A_{2}v_{2}\,\Delta t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6c09bd35f9e8f5dab50d494bf73e37ee3da846b)
