Mathematics desk
< May 18	<< Apr \| May \| Jun >>	May 20 >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

May 19[edit]

Graham's number[edit]

I've been trying to get a handle on the unfathomable size of this thing, so I'll pose the question this way and see if anyone wants to tackle it: if one could write down Graham's number in a book, how big would the book be? --Wyckyd Sceptre 02:21, 19 May 2007 (UTC)[reply]

it's too big a number to think of it that way. Graham's number is much, much larger than the number of atoms in the observable universe (which is on the order of 10⁸⁰). nadav 02:30, 19 May 2007 (UTC)[reply]

Dang, you're right. But the universe is mostly empty space, right? Or are you saying the book is too big to fit in the universe? --Wyckyd Sceptre 03:53, 19 May 2007 (UTC)[reply]

Yes, good point: they're not the same. However, I am fairly certain that Graham's number is indeed so big, that the book will not fit in the observable universe. I haven't done the calculation yet, though. nadav 04:06, 19 May 2007 (UTC)[reply]

OK, here's the calculation. Assume each digit is 3mm wide, 5mm tall, and 0.1 mm thick (the average thickness of paper). This implies that a digit occupies 1.5 x 10^-9 cubic meters. Now, the volume of all space that we can see is 3.4 x 10^80 cubic meters. This implies that if we completely stuffed all of observable space with huuuuge reams of paper, we would be able to fit 2.27 x 10^89 digits. This means that the largest number that we could write out and still fit in observable space is less than 10^(10^90). (See googolplex for a comparable number)

Now let's examine Graham's number, or since we can't look at the number itself, let's look at the tower of powers that appears in that article. That tower has 3^(3^...^3) layers, where the number of 3's in the ellipses is equal to 3^(3^3), which equals about 7.6 x 10^12. So the biggest number that can fit in the observable universe is completely laughable in comparison. It's just not possible to make any physical sense of Graham's number. It is just too big to grasp. nadav 04:50, 19 May 2007 (UTC)[reply]

Yeah, I guess a physical interpretation just isn't feasible. Thanks. --Wyckyd Sceptre 05:12, 19 May 2007 (UTC)[reply]

Not only is the number too big to grasp, it's even impossible to start to grasp how big it is. If you could parcel up the observable universe into (Planck length)³-sized cubes, and write down a digit in every cube, it wouldn't make a dent in writing down the size (number of digits) of the size of the size of ... of the size of the number in conventional decimal notation – let alone the number itself. And the available space would not even suffice to write down the preceding sentence with the ellipsis expanded out far enough to make the sentence false. And yet, compared to almost all natural numbers the number is incredibly small. Makes you think there might be something to ultrafinitism. --Lambiam ^Talk 08:21, 19 May 2007 (UTC)[reply]

You raise an interesting point. With the above discussion in mind, constructivism in general seems so arbitrary. We never really see the objects we are working with, so why even pretend that "construction" is better than the usual way? "God created the integers" yeah right. He mayyyybe made the numbers 1 through googolplex. Everything else is man-made and we can do as we like with it. (Sorry, I'll stop with the soapbox now) nadav 08:47, 19 May 2007 (UTC)[reply]

Where did the size of the universe being 3.4 x 10^80 cubic meters come from? I can't reasily find it elsewhere in wikipedia. -- SGBailey 06:51, 22 May 2007 (UTC)[reply]

That's not the size of the universe, but rather (as stated) the approximate volume of the observable universe. Algebraist 11:33, 22 May 2007 (UTC)[reply]

toroid not a sphere[edit]

is a toroid inversely proportional to a sphere in any type of function that can plot the shape? —The preceding unsigned comment was added by 69.241.236.12 (talk • contribs) 07:20, May 19, 2007 (UTC) - Please sign your posts!

It is not fully clear what the question is. The notion of inverse proportionality is defined between variables denoting quantities. Toroids and spheres are not variables, let alone quantitative variables. If you mean whether one can be transformed into the other by geometric inversion, the answer is no. Such inversions transform spheres into spheres, and toroids into toroids. --Lambiam ^Talk 08:41, 19 May 2007 (UTC)[reply]

Is there anyway to create a torus from an object by subtracting components of a sphere from its' center of mass given equal density distribution of the initial object? I read under torus that it is the product of two circles, however, is it related to a sphere in any way? Lastly, can anyone describe what a 2D sphere is in regard to a n-torus?69.241.236.12 14:57, 19 May 2007 (UTC)Adam[reply]

The torus and sphere are quite different. There is no way to continuously map the surface of a sphere to the surface of a toroid: you have to tear the surface apart to accomplish this. In general, a closed 3D surface with no "loops" can map to a sphere, but with one loop it can map to a torus. The easiest to understand article I could find on wikipedia about this is probably "Simply connected space". (Also, with regard to "components of a sphere"; what do you regard as being a sphere's component?) - Rainwarrior 17:11, 19 May 2007 (UTC)[reply]

A torus is a surface obtained by revolving a circle about a coplanar line in three dimensional space. As the distance from the line to the circle's center approaches zero, the torus will resemble a sphere.

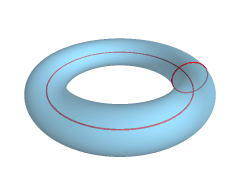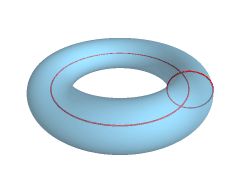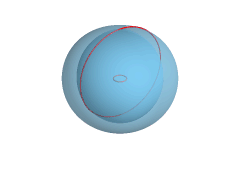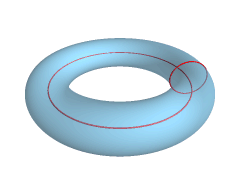
A sphere could be viewed as a degenerate torus, where the radius from the center point to the ring centerline is zero. StuRat 19:54, 19 May 2007 (UTC)[reply]

I don't think I understand you.nadav

Have a look at MathWorld Standard Tori which generalises the concept of a familiar torus. You can view the sphere as a special case of a spindle torus, the torus is wrapped twice around the sphere. --Salix alba (talk) 21:02, 19 May 2007 (UTC)[reply]

I understand now, though I do think it was an unwise choice of nomenclature to use the same word "torus" in the names of topologically distinct surfaces. nadav 21:34, 19 May 2007 (UTC)[reply]

I made an animation to show this, but I guess I was too late. In any case, it may be helpful. — Kieff | Talk 21:44, 19 May 2007 (UTC)[reply]

It's a beautiful animation! Thanks. You should change the caption, though, since if the circle is rotated about a chord then it's no longer a mere topological product. nadav 22:01, 19 May 2007 (UTC)[reply]

Thanks! Feel free to add a better caption and explanation on the image page at Commons, by the way. — Kieff | Talk 22:18, 19 May 2007 (UTC)[reply]

We'll definitely use this once we get a spindle torus article going. nadav 22:05, 19 May 2007 (UTC)[reply]

I'm quite curious as to what software you are using to generate these and other beautiful images I've seen from your hand.

There is one unsatisfactory feature of this torus to sphere maps, namely what happens at the origin. Away from the poles there are two points on the torus which maps to each point on the sphere, however a whole circle on the torus maps to each pole. If it were not for these points we would have a double cover of the sphere, but alas no. I don't know if its possible, I suspect not.

Someone mentioned inversion in a sphere, which leads us to consider cyclides, which are formed by inversion of a torus in a sphere. Inversion of the spindle and horned torus are particularly nice as after inversion the self intersecting parts can appear on the outside of the surface. --Salix alba (talk) 23:42, 19 May 2007 (UTC)[reply]

You're right to say it's not possible for such a cover to exist, as the sphere (being simply connected) is it's own universal cover. nadav 02:14, 20 May 2007 (UTC)[reply]

I'm using POV-Ray. Great program! — Kieff | Talk 01:16, 20 May 2007 (UTC)[reply]

I'm pretty sure you can't have a 2D sphere, by definition. --140.247.242.30 20:52, 19 May 2007 (UTC)[reply]

I think the propper term is 2-Sphere, which is used to denote the normal sphere in the set of n-spheres. Its also important to distinguish a sphere, whih is just the surface with the Ball (mathematics) which contains the interior. --Salix alba (talk) 21:02, 19 May 2007 (UTC)[reply]

Also, unlike the term n-sphere, for an n-torus the n is not related to the number of dimensions, but rather how many holes it has. A 2-torus has two holes (kind of like a figure 8) and a 3-torus has 3, etc. - Rainwarrior 21:44, 19 May 2007 (UTC)[reply]

That too, but not always. Our article on torus also covers that. — Kieff | Talk 01:16, 20 May 2007 (UTC)[reply]

Oh, that's interesting. I'd never seen that notation used for a variable-dimensional torus before. Well, I guess it's both then. - Rainwarrior 04:35, 20 May 2007 (UTC)[reply]

Is this a question about geometric modelling, more specifically 3D modelling in 3D computer graphics? There is no obvious way of getting a torus from spheres using standard operations. You could flatten a ball into an oblate spheroid and then subtract another ball, resulting in a shape that is topologically a solid torus, but its surface is not smooth. Or you can take the Minkowski sum of a circle and a ball that has a smaller radius, giving a smooth solid torus. --Lambiam ^Talk 21:46, 19 May 2007 (UTC)[reply]

Doug DeCarlo looked at transforming ("morphing") sphere to torus within computer graphics. More broadly, Jon Hart and others are doing some pretty research in "computational topology". Decades ago, Nelson Max produced the first computer graphic animation of a smooth sphere eversion, part of a long history of beautiful collaboration between computer graphicists and mathematicians (especially topologists). The prettiest connection between torus and sphere is with S³, not S², and here Tom Banchoff is the pioneer. --KSmrq^T 05:49, 20 May 2007 (UTC)[reply]

MATHEMATICS[edit]

what is 1/infinity multiplied by 1/0?

Undefined. You can't do math on infinity. For example, 2 times infinity still equals infinity. Anything divided by zero is also infinity, so you can't do math with that, either. StuRat 19:49, 19 May 2007 (UTC)[reply]

(edit conflict) The short answer to your question is that there is no one defined meaning for the expression

{\frac {1}{0}}\cdot {\frac {1}{\infty }}

, because the laws of field operations do not allow dividing 1 by 0, and infinity is not even a real number. Sometimes mathematicians do allow expressions of this form (see Projectively extended real numbers), and they define 1/0 to equal infinity and 1/∞ to equal zero. However, even in that case, there is no definition for multiplication of 0 by ∞. The reason for this is that expressions using ∞ are defined through the use of limits, and the limit

\lim _{x\to 0,y\to \infty }xy

does not exist. For example, let's say I decide to let y go to infinity by setting it equal to 1/x. Then the limit happens to equal 1. But I could just as easily set y equal to 2/x, and then conclude that the limit would equal two. But we can't allow the limit to equal more than one number; and for this reason, we can't define the product of 0 and infinity. nadav 20:16, 19 May 2007 (UTC)[reply]

A small correction:

{\tfrac {1}{0}}

is not defined in the extended real numbers. It is defined, however, in the real projective line. Even there, not anything divided by zero is infinity, the exception being of course

{\tfrac {0}{0}}

. -- Meni Rosenfeld (talk) 22:57, 19 May 2007 (UTC)[reply]

Good point. I was not careful about where the links went. I've fixed it now. nadav 23:05, 19 May 2007 (UTC)[reply]

Multilateration[edit]

Can someone tell me the equation for X, Y, and Z of the emitter are in Multilateration, I tried (with others as help) my best at solving but it's just very complicated, and simply becomes a huge equation, maybe one of you knows a sort-cut? Thanks, Jeffrey.Kleykamp 20:45, 19 May 2007 (UTC)[reply]

If you have four points (as in the article) and your measurements give you only the differences between distances from the emitter to other points (again, as in the article), then I don't think there is a shortcut. I would not try to solve this algebraically, but use numerical methods. If you can synchronize the emitter and the receivers, and know the times not only of when the signal is received but also when it is emitted, you can measure the distances themselves (in which case three non-collinear receivers suffice except for reflection with respect to the plane through the three receivers; see trilateration), and an algebraic shortcut is possible. --Lambiam ^Talk 22:10, 19 May 2007 (UTC)[reply]

Yes, however that is beside the point because I simply don't know anything about the emitter and therefore need Multilateration. Thanks anyway, Jeffrey.Kleykamp 22:38, 19 May 2007 (UTC)[reply]