Wikipedia:Reference desk/Archives/Mathematics/2009 October 18

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

October 18

Getting pi with a limit

I was reading Method of exhaustion, and I wanted to try out Archimedes' method for calculating pi with a limit. Finding the limit as the number of sides of a regular polygon approaches infinity of the ratio of its area to its apothem squared gave me:

$\lim _{n\to \infty }\ n\tan \left({\frac {180^{\circ }}{n}}\right)$

Obviously, this equals pi, but I have no clue how to show that. I only have a very basic understanding of limits; could someone show me how to evaluate that expression to obtain pi? Thegreenj 00:04, 18 October 2009 (UTC)

If you know about derivatives, your limit is just the derivative of tan(πx) at x=0, π indeed. That's not Archimede's method, of course. He compared the perimeter of the inscribed and of the circumscribed regular n-gons, that are very close for large n -and π is in between. If n is a power of two, meaning that you double the vertices recursively, the formula for the perimeter is somehow simpler, giving rise to Viète's formula. --78.13.138.118 (talk) 00:20, 18 October 2009 (UTC)

Remember that tan = opp/adj. Suppose the circle has unit radius, as you often do in trigonometry. Draw the triangle in which the "adjacent" side is from (0,0) to (1,0) and the "opposite" side is a vertical line of height tan(180°/n). Then the angle between "adjacent" and "hypotenuse" is 180°/n (draw the picture). That side is longer than the arc of the circle between the "adjacent" side and the hypotenuse. Stack up n of these, going counterclockwise from the positive half of the x-axis to the negative half. The sum of the lengths of those "opposite" sides is n tan(180°/n). And it approaches the length of the arc. Michael Hardy (talk) 00:49, 18 October 2009 (UTC)

• Thanks to both of you, though I admit I don't wholly understand 78.13.138.118's response, and I seem to have misunderstood Archimedes' method (the text and the graphic in the article are different methods). Thegreenj 01:52, 19 October 2009 (UTC)

The value of $\tan(x)$ at $x=0$ is 0, and the derivative of $\tan$ at $x=0$ is 1. Consider $x:={\frac {\pi }{n}}$, that goes to 0 as $n$ goes to infinity: then

$\lim _{n\to \infty }n\tan \left({\frac {\pi }{n}}\right)=\lim _{n\to \infty }\pi {\frac {\tan \left({\frac {\pi }{n}}\right)}{\frac {\pi }{n}}}=\lim _{x\to 0}\pi {\frac {\tan(x)}{x}}=\pi \lim _{x\to 0}{\frac {\tan(x)-\tan(0)}{x}}=\pi {\frac {\mathrm {d} }{\mathrm {d} x}}\tan(x){\Big |}_{x=0}=\pi .$

Archimedes compared π with the perimeters of the inscribed and the circumscribed 96-sided regular polygons, getting the celebrated bounds 3+10/71 < π < 3+1/7. The choice of 96 = 3·2⁵ corresponds to starting with an equilateral triangle and bisecting 5 times. PS: Indeed you are rigth about the article being a bit unclear: Archimedes did not use exhaustion to compute π, but to prove the formula πr² for the area inside a circle, that is, to prove that the ratio of a circle to a square with edge equal to the radius is the same as the ratio of the circumference to the diameter, that is π. And, of course, the bounds he gave on π use no exhaustion. (Fixed). --pma (talk) 10:39, 19 October 2009 (UTC)

Application of the PNT to a sequence of numbers

82818079787776757473727170696867666564636261605958575655545352515049484746454443424140393837363534333231302928272625242322212019181716151413121110987654321 has just been determined to be the only prime in the implied sequence up to the thousandth term. However, it seems to me by using the PNT that there should be infinitely many primes in the sequence, with the probability of each third (two out of three have 3 dividing them) term being prime going like C/D, where D is the number of digits and C is a constant. Is this right?Julzes (talk) 04:10, 18 October 2009 (UTC)

Yes that's surprising. Scrubbed my reply after thinking more about it. I thought you'd get 2/7 removed for factor 7 etc but my reasoning doesn't follow Dmcq (talk) 10:38, 18 October 2009 (UTC)

It seems a little tricky to determine the constant, since you have clear conditioning for the primes 2, 3, and 5 (never divisible by 2 or 5, and also never by 3 for the terms worth looking at). It's possible to use modularity for other primes too, I suppose, to eliminate other sets of numbers. Right now I'm looking at whether I can get a second term in the sequence. Perhaps someone might be interested in taking a more certain route (or less human-intensive) than the one I am, which is to simply keep trying numbers input by prefixing three numbers at alpertron.com. The base-7 case also looks intriguing. I know there is no solution up to the term beginning 1000 (=343), and only a much smaller fraction of cases are even worth looking at. First terms are trivial for bases 2 through 6, but that is about all I know about the alternative base problem.Julzes (talk) 11:34, 18 October 2009 (UTC)

I posted at User talk:PrimeHunter#New Prime Discovered. I guess you mean http://www.alpertron.com.ar/ECM.HTM. That applet is designed for finding prime factors and is relatively slow at primality testing. PrimeHunter (talk) 14:53, 18 October 2009 (UTC)

This is Sloane A000422. Dmcq (talk) 16:59, 18 October 2009 (UTC)

Can kite be a trapezium?

A kite.

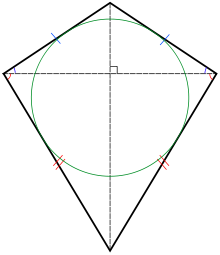
Kite is a quadrilateral which has two pairs of adjacent sides equal. By any means can a kite become a trapezium or trapezoid i.e. two of its opposite sides are parallel? Srinivas 10:23, 18 October 2009 (UTC)

See square. --Tango (talk) 11:08, 18 October 2009 (UTC)

No, no, I mean it should be a kite only i.e. adjacent sides only must be equal and opposite sides must be unequal. What Tango (talk · contribs) said is also correct as square is a kite but I forgot to mention that opposite sides must be unequal and only adjacent sides must be equal. Srinivas 12:50, 18 October 2009 (UTC)

Any kite which is also a trapezoid must be a rhombus. Let the kite be ABCD where AB = BC and CD = DA and suppose AB is parallel to CD. Draw the two diagonal AC and BD and let O be the point of intersection. By alternate angles, angle OCD = angle OAB. Then by angle-side-angle, traingle OAB is congruent to triangle OCD, so AB = CD and all four sides are equal. It's a cute problem and it might work as an extra credit in a high geometry class.--RDBury (talk) 13:29, 18 October 2009 (UTC)

Thanks a lot, RDBury (talk · contribs), you solved my doubt clearly. Srinivas 14:38, 18 October 2009 (UTC)

Smallest number which have the first n positive integers as divisors

Is there are name for the numbers which are the smallest to have the first n positive integers as divisors? 88.104.157.141 (talk) 11:46, 18 October 2009 (UTC)

Sloane's just calls the lcms of {1, 2, ..., n}, so if there is a specific name, it can't be very widely used. Algebraist 11:54, 18 October 2009 (UTC)

Aside from the formula (name?) lcm(2,3,...,n), it could also be written as a simple product of primorials. I can't get it into notation, but it's the product from i=1 to infinity of the product of the primes less than or equal to n^(1/i). If I were naming it I would call it the "superprimorial up to n" or something. "Least common multiple of the numbers up to n" is clearer and almost as short, though.Julzes (talk) 12:08, 18 October 2009 (UTC)

Its logarithm has a name - it is the second Chebyshev function ψ(n). Gandalf61 (talk) 13:21, 18 October 2009 (UTC)

Modular forms: Finding the fundamental domain for a finite index subgroup

Resolved

Argh, I can not believe I closed this window when I was almost done with my question! :) I will just write it shorter this time.

First, I must give some background. I know any matrix in SL(2, Z) can be written uniquely in the form

$T=(-1)^{r}P^{2p_{0}}VP^{2p_{1}}V\cdots VP^{2p_{n}},$

where $P={\begin{bmatrix}0&-1\\1&1\end{bmatrix}}$ and $V={\begin{bmatrix}0&-1\\-1&0\end{bmatrix}}$. Based on this representation, define $h(T)=n+2r$ for any matrix in SL(2, Z). Now, consider

$\Gamma ^{4}=\{T\in SL(2,\mathbb {Z} ):h(T)\equiv 0\mod 4\}.$

My understanding is, to get the fundamental domain of this subgroup of SL(2, Z), which is index 4 by the way, I will need to find a set of coset representatives and apply each to the "standard" fundamental domain of SL(2, Z), which is the hyperbolic triangle with vertices $\infty ,{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}},-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}$. Then, the union of the 4 images I get will be a fundamental domain of $\Gamma ^{4}$.

So, my question: How do I figure out the 4 coset representatives. Obviously the identity matrix is one of them. I know of several standard matrices from the book I am using that are not in this group, so of course these are candidates for the other 3 representatives:

$U=P^{0}VP^{4},(n+2r=1),\qquad V=P^{0}VP^{0}(n+2r=1),\qquad W=-P^{0}VP^{2}(n+2r=2),\qquad P=-P^{4}(n+2r=1)$

I noticed that $-I\Gamma ^{4}$ is going to be the set of all matrices with $h(T)\equiv 2\mod 4$ since it just increases or decreases r by 1. And, I believe that $V\Gamma ^{4}$is all those with $h(T)\equiv 1\mod 4$, and then $-V\Gamma ^{4}$ is all those with $h(T)\equiv 3\mod 4$, unless I messed something up. So, it seems as if $\pm I,\pm V$ would be a set of coset representatives. But, the action of $-I$ is trivial on the upper half plane so I end up with only two different images of the "standard" fundamental domain of SL(2, Z), and not 4. Am I doing something wrong here? Or is it fine that I end up with only two copies of that? StatisticsMan (talk) 21:26, 18 October 2009 (UTC)

What's going on is that, since the element $-I$ acts trivially, it's really the quotient group PSL(2,Z) = SL(2,Z)/$\{I,-I\}$ that's acting on the hyperbolic plane. The image of Γ⁴ in this quotient group has index 2, which is why the fundamental domain that you're getting only has two triangles. Jim (talk) 04:27, 19 October 2009 (UTC)

Okay, I figured that was it but I was not sure if that was okay. Thanks a lot! StatisticsMan (talk) 01:17, 20 October 2009 (UTC)

Use of abacus in United States education

I was reading an article on the abacus:

http://en.wikipedia.org/wiki/Abacus#School_abacus

When was the abacus first used in the United States education system to teach counting skills and things like this?

Thanks for the help!

137.81.112.223 (talk) 23:23, 18 October 2009 (UTC)