Wikipedia:Reference desk/Archives/Mathematics/2010 August 8
| Mathematics desk | ||
|---|---|---|
| < August 7 | << Jul | August | Sep >> | August 9 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
August 8[edit]
What is Cr norm of the space of maps from X to Y[edit]
X and Y are both metric space. Thanks a lot! 155.69.135.100 (talk) 12:26, 8 August 2010 (UTC)
elliptic curves[edit]
On page 13 0f "Elliptic Curves" by Dale Husemuller (1986) I read the following: "As for cubics, there is no known method for determining, in a finite number of steps, whether there is a rational point on a given cubic curve. This important question is still open."
My question is whether a method has been found, and if that is the case, where do I find such a method?
amri@vianet.ca --66.225.171.69 (talk) 16:23, 8 August 2010 (UTC)
- I have the second edition, 2004, and it says the same thing. I'm pretty sure it's still true and has to do with the fact that finding the rank of an elliptic curve is very hard. This includes even showing that the rank is 0 being difficult. So, assume so elliptic curve has no points of finite order (which I think is not too hard to determine... but don't quote me on that), then the question is, does it have any points of infinite order. And, if you can't see any obvious ones just by looking at the equation (like clearly y^2 = x^3 - 4x has some solutions you can see without doing any work), then it may be very hard to determine if that elliptic curve has zero points or an infinite number and there is no one method that always works to answer the question. StatisticsMan (talk) 18:31, 8 August 2010 (UTC)
Simple Set Theory[edit]
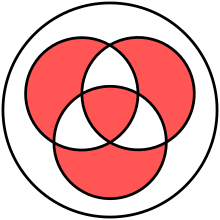
I know that we're lucky to have many talented set theorists on this page, so I'm sure my question will be answered in no time. Given a set X, take two subsets, say A and B, and consider the union A ∪ B and the intersection A ∩ B. For a set C ⊆ A, let A − C = {a ∈ A : a ∉ C}. Let P(X) denote the power set of X. Define a binary operation ƒ : P(X) × P(X) → P(X) given by ƒ(A,B) = (A ∪ B) − (A ∩ B). Notice that this is well defined since A ∩ B ⊆ A ∪ B. Let us write A⋅B in place of ƒ(A,B). I want to show that this binary operation is associative, i.e. for any subsets, A, B and C, of the set X we have (A⋅B)⋅C = A⋅(B⋅C). Explicitly this associativity condition becomes:
- { ( [A ∪ B] − [A ∩ B] ) ∪ C } − { ( [A ∪ B] − [A ∩ B] ) ∩ C } = { A ∪ ( [B ∪ C] − [B ∩ C] ) } − { A ∩ ( [B ∪ C] − [B ∩ C] ) }.
I've done some examples with Venn Diagrams and it seems to be true. The figure that I've included shows (A⋅B)⋅C = A⋅(B⋅C) in red, when A, B and C were solid disks. It doesn't matter which way I do it; I get the same set. I was hoping that someone might be able to help me with the following.
- Does the operation A − C, where C ⊆ A and A − C = {a ∈ A : a ∉ C}, have a name?
- Can we prove formally that (A⋅B)⋅C = A⋅(B⋅C) for all A, B, C ∈ P(X), and if so − how?
I thank you all in advance for what I am sure will be your helpful and well-thought replies. — Fly by Night (talk) 19:53, 8 August 2010 (UTC)
- The first operation is called set difference or set subtraction. Your f is called the symmetric difference. An easy way to see that it's associative is to note that, if you temporarily identify subsets of X with functions from X to {0,1}, where the value is 1 if the element is in the subset and 0 if it isn't, then the symmetric difference corresponds exactly to addition mod 2. --Trovatore (talk) 20:07, 8 August 2010 (UTC)
- Thanks for that, Trovatore. The symmetric difference gives a group operation on P(X). (The identity element is the empty set ∅, and all sets are their own inverses: A⋅A = ∅. Are there any group theoretic results then about P(X)? What about representation theory? (I came up with this idea yesterday while trying to give a group structure to a topology (X,Σ), but that doesn't work because the symmetric difference of open sets need not be open. If you replace Σ – the set of open sets – by P(X) then you're in business). — Fly by Night (talk) 22:10, 8 August 2010 (UTC)
- Thanks Tango, but if it's clear – which it is – then there's no point in mentioning it. I was hoping for something interesting and less obvious. For example, do any theorems from group theory translate into non-obvious theorems about set theory, etc. Also, as my reply to Trovatore said: I was trying to give group structures to topologies, so finite sets weren't really what I had in mind. — Fly by Night (talk) 23:18, 8 August 2010 (UTC)
- The point in mentioning it was that the classification theorem I invoked only applies to abelian groups. It's good practice in mathematics to always be explicit about the premises of a theorem being met before invoking the theorem. --Tango (talk) 23:38, 8 August 2010 (UTC)
- True, but irrelevant. You're still no closer to answering my question in a non-trivial way. I appreciate you making the effort to write a reply, but it wasn't really what I was looking for. Thanks again. — Fly by Night (talk) 00:04, 9 August 2010 (UTC)
- Identifying the group has to be the first step in finding out if it can tell you anything useful. --Tango (talk) 00:06, 9 August 2010 (UTC)
- I very much doubt that you will be able to "identify the group". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to learn something new. Better that we leave it here, Tango. Thanks all the same. — Fly by Night (talk) 00:12, 9 August 2010 (UTC)
- Algebraist has identified the group (see below): it's . --Tango (talk) 00:27, 9 August 2010 (UTC)
- Exactly: Algebraist has identified the group. You were talking about finite groups when I had general topologies in mind. That's why I got a frustrated. I apologise for letting things annoy me so easily. — Fly by Night (talk) 22:25, 9 August 2010 (UTC)
- Algebraist has identified the group (see below): it's . --Tango (talk) 00:27, 9 August 2010 (UTC)
- I very much doubt that you will be able to "identify the group". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to learn something new. Better that we leave it here, Tango. Thanks all the same. — Fly by Night (talk) 00:12, 9 August 2010 (UTC)
- Identifying the group has to be the first step in finding out if it can tell you anything useful. --Tango (talk) 00:06, 9 August 2010 (UTC)
- True, but irrelevant. You're still no closer to answering my question in a non-trivial way. I appreciate you making the effort to write a reply, but it wasn't really what I was looking for. Thanks again. — Fly by Night (talk) 00:04, 9 August 2010 (UTC)
- The point in mentioning it was that the classification theorem I invoked only applies to abelian groups. It's good practice in mathematics to always be explicit about the premises of a theorem being met before invoking the theorem. --Tango (talk) 23:38, 8 August 2010 (UTC)
- There is an obvious isomorphism between P(X) and the direct product of |X| copies of Z2: just replace sets with their indicator functions, as Trovatore suggested. Algebraist 22:52, 8 August 2010 (UTC)
- Thanks Tango, but if it's clear – which it is – then there's no point in mentioning it. I was hoping for something interesting and less obvious. For example, do any theorems from group theory translate into non-obvious theorems about set theory, etc. Also, as my reply to Trovatore said: I was trying to give group structures to topologies, so finite sets weren't really what I had in mind. — Fly by Night (talk) 23:18, 8 August 2010 (UTC)
- Here's the thing Algebraist... if it's obvious, then there's no point in mentioning it. StatisticsMan (talk) 02:49, 9 August 2010 (UTC)
- I know. I am referencing a comment from above by Fly By Night who told Tango he didn't need to point out anything that was clearly true. StatisticsMan (talk) 16:35, 9 August 2010 (UTC)
Thanks to everyone for their answers. I now consider my question to be resolved. Thanks to Trovatore, Tango and Algebraist for their, as ever, insightful comments. I'm also going to archive the thread because I don't think it's moving in such a positive direction. Seeing as the question has been resolved in the OP's eyes, I don't see any problem in archiving. Thanks again to everyone. — Fly by Night (talk) 22:25, 9 August 2010 (UTC)
- (Archiving was since removed by Meni Rosenfeld. — Fly by Night (talk) 21:56, 10 August 2010 (UTC))



