Draft:One-step method

One-step methods approximate the solution (blue) of an initial value problem by starting from the given starting point $A_{0}$ from the given starting point $A_{1}$, $A_{2}$ etc. can be determined

In numerical mathematics, one-step methods and multi-step methods are a large group of calculation methods for solving initial value problems. This problem, in which an ordinary differential equation is given together with an initial condition, plays a central role in all natural and engineering sciences and is also becoming increasingly important in the economic and social sciences, for example. Initial value problems are used to analyze, simulate or predict dynamic processes.

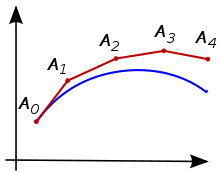
The basic idea behind one-step methods is that they calculate approximation points step by step along the desired solution, starting from the given starting point. They only use the most recently determined approximation for the next step, in contrast to multi-step methods, which also include points further back in the calculation. The one-step methods can be roughly divided into two groups: the explicit methods, which calculate the new approximation directly from the old one, and the implicit methods, which require an equation to be solved. The latter are also suitable for so-called stiff initial value problems.

The simplest and oldest one-step method, the explicit Euler method, was published by Leonhard Euler in 1768. After a group of multi-step methods was presented in 1883, Carl Runge, Karl Heun and Wilhelm Kutta developed significant improvements to Euler's method around 1900. These gave rise to the large group of Runge-Kutta methods, which form the most important class of one-step methods. Further developments in the 20th century include the idea of extrapolation and, above all, considerations on step width control, i.e. the selection of suitable lengths for the individual steps of a method. These concepts form the basis for solving difficult initial value problems, as they occur in modern applications, efficiently and with the required accuracy using computer programs.

Introduction

Ordinary differential equations

The development of differential and integral calculus by the English physicist and mathematician Isaac Newton and, independently of this, by the German polymath Gottfried Wilhelm Leibniz in the last third of the 17th century was a major impetus for the mathematization of science in the early modern period. These methods formed the starting point of the mathematical subfield of analysis and are of central importance in all natural and engineering sciences. While Leibniz was led to differential calculus by the geometric problem of determining tangents to given curves, Newton started from the question of how changes in a physical quantity can be determined at a specific point in time.

For example, when a body moves, its average speed is simply the distance traveled divided by the time required to travel it. However, in order to mathematically formulate the instantaneous velocity ${\textstyle v(t)}$of the body at a certain point in time $t$ , a limit transition is necessary: Consider short time spans of length $\Delta t$ , the distances traveled $\Delta x$ and the corresponding average velocities ${\tfrac {\Delta x}{\Delta t}}$.If the time period Δ 𝑡 is now allowed to converge towards zero and if the average velocities also approach a fixed value, then this value is called the (instantaneous) velocity ${\textstyle v(t)}$ at the given time $t$. If $\Delta t$denotes the position of the body at time 𝑡 , then write $v(t)=x'(t)$and call $v$ the derivative of $x$ .

The decisive step in the direction of differential equation models is now the reverse question: In the example of the moving body, let the velocity ${\textstyle v(t)}$ be known at every point in time 𝑡 and its position $x(t)$ be determined from this. It is clear that the initial position of the body at a point in time 𝑡 0 must also be known in order to be able to solve this problem unambiguously. We are therefore looking for a function $x(t)$ with $x'(t)=v(t)$ that fulfills the initial condition $x'(t)=v(t)$ with given values $t_{0}$ and $x_{0}$.

In the example of determining the position 𝑥 of a body from its velocity, the derivative of the function being searched for is explicitly given. In most cases, however, the important general case of ordinary differential equations exists for a sought-after variable $y$: Due to the laws of nature or the model assumptions, a functional relation is known that specifies how the deriativey $y'(t)$ of the function to be determined can be calculated from $t$ and from the (unknown) value $y(t)$ . In addition, an initial condition must again be given, which can be obtained, for example, from a measurement of the required variable at a fixed point in time. To summarize, the following general type of task exists: Find the function $y$ that satisfies the equations

$y'(t)=f(t,y(t)),\quad y(t_{0})=y_{0}$

is fulfilled, where $f$ is a given function.

The shown solution of the differential equation of the Lorenz attractor is a very complicated curve in three-dimensional space

A simple example is a variable $y$ that grows exponentially. This means that the instantaneous change, i.e. the derivative $y'(t)$, is proportional to $y(t)$ itself. Therefore, $y'(t)=\lambda y(t)$ with a growth rate $\lambda$ and, for example, an initial condition $y(0)=y_{0}$ . In this case, the required solution 𝑦 can already be found using elementary differential calculus and specified using the exponential function: $y(t)=y_{0}e^{\lambda t}$.

The required function $y$ in a differential equation can be vector-valued, i.e. for each $t$, $y(t)=(y_{1}(t),\dotsc ,y_{d}(t))$ can be a vector with $d$ components. This is also referred to as an $d$ -dimensional system of differential equations. In the case of a moving body, $y(t)$ is its position in $d$ -dimensional Euclidean space and $y'(t)$ is its velocity at time $t$ . The differential equation therefore specifies the velocity of the trajectory with direction and magnitude at each point in time and space. The trajectory itself is to be calculated from this.

Basic idea of the one-step procedure

In the simple differential equation of exponential growth considered above as an example, the solution function could be specified directly. This is generally no longer possible for more complicated problems. Under certain additional conditions, it is then possible to show that a clearly determined solution to the initial value problem exists for the function $f$; however, this can then no longer be explicitly calculated using solution methods of analysis (such as separation of variables, an exponential approach or variation of the constants). In this case, numerical methods can be used to determine approximations for the solution sought.

The methods for the numerical solution of initial value problems of ordinary differential equations can be roughly divided into two large groups: the one-step and the multi-step methods. Both groups have in common that they calculate approximations $y_{0},y_{1},y_{2},\dotsc$ for the desired function values $y(t_{0}),y(t_{1}),y(t_{2}),\dotsc$ at points$t_{0}<t_{1}<t_{2}<\ldots$ step by step. The defining characteristic of one-step methods is that only the "current" approximation $y_{j+1}$ is used to determine the following approximation $y_{j}$ . In contrast, multi-step methods also include previously calculated approximations; a three-step method would therefore use $y_{j-1}$ and $y_{j-2}$ to determine the new approximation $y_{j+1}$ in addition to $y_{j}$ .

Two steps of the explicit Euler method

The simplest and most basic one-step method is the explicit Euler method, which was introduced by the Swiss mathematician and physicist Leonhard Euler in 1768 in his textbook Institutiones Calculi Integralis. The idea of this method is to approximate the solution sought by a piecewise linear function in which the gradient of the straight line piece is given by $t_{j}$ in each step from the point math>t_{j+1}</math> to the point $f(t_{j},y_{j})$. In more detail: The problem definition already gives a value of the function being searched for, namely $y(t_{0})=y_{0}$ . However, the derivative at this point is also known, as $y'(t_{0})=f(t_{0},y_{0})$ applies. This allows the tangent to the graph of the solution function to be determined and used as an approximation. At the point $t_{1}>t_{0}$ the following results with the step size $h_{0}:=t_{1}-t_{0}$

$y(t_{1})\approx y_{0}+h_{0}f(t_{0},y_{0})=:y_{1}$.

This procedure can now be continued in the following steps. Overall, this results in the following calculation rule for the explicit Euler method

$y_{j+1}=y_{j}+h_{j}f(t_{j},y_{j}),\quad j=0,1,2,\dotsc$

with the increments $h_{j}=t_{j+1}-t_{j}$.

The explicit Euler method is the starting point for numerous generalizations in which the gradient $f(t_{j},y_{j})$ is replaced by gradients that approximate the behaviour of the solution between the points $t_{j}$ and $t_{j+1}$ more precisely. An additional idea for one-step methods is provided by the implicit Euler method, which uses $f(t_{j+1},y_{j+1})$ as the gradient. At first glance, this choice does not seem very suitable, as $y_{j+1}$ is unknown. However, as a procedural step, we now obtain the equation

$y_{j+1}=y_{j}+h_{j}f(t_{j+1},y_{j+1})$

from which $y_{j+1}$ can be calculated (using a numerical method if necessary). If, for example, the arithmetic mean of the slopes of the explicit and implicit Euler method is selected as the slope, the implicit trapezoidal method is obtained. In turn, an explicit method can be obtained from this if, for example, the unknown $y_{j+1}$ on the right-hand side of the equation is approximated using the explicit Euler method, the so-called Heun method. All these methods and all other generalizations have the basic idea of one-step methods in common: the step

$y_{j+1}=y_{j}+h_{j}\Phi$

with a gradient $\Phi$ that can depend on $t_{j}$ , $y_{j}$ and $h_{j}$ as well as (for implicit methods) on $y_{j+1}$.

Definition

With the considerations from the introductory section of this article, the concept of the one-step method can be defined as follows: Let the solution $y$ of the initial value problem be sought

$y'(t)=f(t,y(t))$, $\quad y(t_{0})=y_{0}$.

It is assumed that the solution

$y\colon I\to \mathbb {R} ^{d}$

exists on a given interval $I=[t_{0},T]$ and is uniquely determined. Are

$t_{0}<t_{1}<t_{2}<\ldots <t_{n}=T$

Intermediate positions in the interval $I$ and $h_{j}=t_{j+1}-t_{j}$ the corresponding increments, then this is given by

$y_{j+1}=y_{j}+h_{j}\Phi (t_{j},y_{j},y_{j+1},h_{j})$, $\quad j=0,\dotsc ,n-1$

given method is a one-step method with method function $\Phi$ . If $\Phi$ does not depend on $y_{j+1}$, then it is called an explicit one-step method. Otherwise, an equation for $j$ must be solved in each step $j$ and the method is called implicit.

Consistency and convergence

Convergence order

For a practical one-step procedure, the calculated $y_{j}$ should be good approximations for the values $y(t_{j})$ of the exact solution $y$ at the point $t_{j}$ . As the variables are generally $d$ -dimensional vectors, the quality of this approximation is measured using a vector norm as $\|y_{j}-y(t_{j})\|$ , the error at the point $t_{j}$ . It is desirable that these errors quickly converge to zero for all $j$ if the step sizes are allowed to converge to zero. In order to also capture the case of non-constant step sizes, $h$ is defined more precisely as the maximum of the step sizes used and the behavior of the maximum error at all points $j$ is considered in comparison to powers of $h$ . The one-step method for solving the given initial value problem is said to have the order of convergence $p\geq 1$ if the estimate

$\max _{j=0,\dotsc ,n}\|y_{j}-y(t_{j})\|\leq Ch^{p}$

applies to all sufficiently small $h$ with a constant $C>0$ that is independent of $h$. The order of convergence is the most important parameter for comparing different one-step methods. A method with a higher order of convergence $p$ generally delivers a smaller total error for a given step size or, conversely, fewer steps are required to achieve a given accuracy. For a method with $p=1$, it is to be expected that the error will only be approximately halved if the step size is halved. With a method of convergence order $p=4$, on the other hand, it can be assumed that the error is reduced by a factor of approximately ${\bigl (}{\tfrac {1}{2}}{\bigr )}^{4}={\tfrac {1}{16}}$.

Global and local error

The errors $\|y_{j}-y(t_{j})\|$ considered in the definition of the convergence order are made up of two individual components in a way that initially seems complicated: On the one hand, of course, they depend on the error that the method makes in a single step by approximating the unknown gradient of the function being searched for by the method function. On the other hand, however, it must also be taken into account that the starting point $(t_{j},y_{j})$ of a step generally does not match the exact starting point $(t_{j},y(t_{j}))$; the error after this step therefore also depends on all errors that have already been made in the previous steps. Due to the uniform definition of the one-step procedures, which differ only in the choice of the procedure function $\Phi$, it can be proven, however, that (under certain technical conditions at $\Phi$ ) one can directly infer the order of convergence from the error order in a single step, the so-called consistency order.

The concept of consistency is a general and central concept of modern numerical mathematics. While the convergence of a method involves investigating how well the numerical approximations match the exact solution, in simplified terms the "reverse" question is asked in the case of consistency: How well does the exact solution fulfill the method specification? In this general theory, a method is convergent if it is consistent and stable. To simplify the notation, the following consideration assumes that an explicit one-step procedure

$y_{j+1}=y_{j}+h\Phi (t_{j},y_{j},h)$

with a constant step size $h$ exists. With the true solution $t\mapsto y(t)$, the local truncation error (also called local process error) $\eta$ is defined as

$\eta (t,h)=y(t)+h\Phi (t,y(t),h)-y(t+h)$.

Thus, one assumes that the exact solution is known, starts a method step at the point $(t,y(t))$ and forms the difference to the exact solution at the point $t+h$. This defines: A one-step method has the consistency order $p\geq 1$ if the estimate

$\|\eta (t,h)\|\leq Ch^{p+1}$

applies to all sufficiently small $h$ with a constant $C>0$ that is independent of $h$.

The striking difference between the definitions of the consistency order and the convergence order is the power $h^{p+1}$ instead of $h^{p}$ . This can be clearly interpreted as meaning that a power of the step size is "lost" during the transition from local to global error. The following theorem, which is central to the theory of one-step methods, applies:

If the process function $\Phi$ is Lipschitz-continuous and the associated one-step process has the consistency order $p$ , then it also has the convergence order $p$ .

The Lipschitz continuity of the process function as an additional requirement for stability is generally always fulfilled if the function $f$ from the differential equation itself is Lipschitz-continuous. This requirement must be assumed for most applications anyway in order to guarantee the unambiguous solvability of the initial value problem. According to the theorem, it is therefore sufficient to determine the consistency order of a one-step method. In principle, this can be achieved by Taylor expansion of $\eta (t,h)$ to powers of $h$. In practice, the resulting formulas for higher orders become very complicated and confusing, so that additional concepts and notations are required.

Stiffness and A-stability

The convergence order of a method is an asymptotic statement that describes the behavior of the approximations when the step size converges to zero. However, it says nothing about whether the method actually calculates a useful approximation for a given fixed step size. Charles Francis Curtiss and Joseph O. Hirschfelder first described in 1952 that this can actually be a major problem for certain types of initial value problems. They had observed that the solutions to some differential equation systems in chemical reaction kinetics could not be calculated using explicit numerical methods and called such initial value problems "stiff". There are numerous mathematical criteria for determining how stiff a given problem is. Stiff initial value problems are usually systems of differential equations in which some components become constant very quickly while other components change only slowly. Such behavior typically occurs in the modeling of chemical reactions. However, the most useful definition of stiffness for practical applications is: An initial value problem is stiff if, when solving it with explicit one-step methods, the step size would have to be chosen "too small" in order to obtain a useful solution. Such problems can therefore only be solved using implicit methods.

Zur Berechnung einer exponentiell fallenden Lösung (blau) ist das explizite Euler-Verfahren (rot) bei zu großer Schrittweite völlig unbrauchbar; das implizite Euler-Verfahren (grün) bestimmt die Lösung für beliebige Schrittweiten qualitativ richtig.

This effect can be illustrated more precisely by examining how the individual methods cope with exponential decay. According to the Swedish mathematician Germund Dahlquist, the test equation

$y'(t)=\lambda y(t),\quad y(0)=1$

with the exponentially decreasing solution $\lambda <0$ for $y(t)=e^{\lambda t}$. The adjacent diagram shows - as an example for the explicit and implicit Euler method - the typical behavior of these two groups of methods for this seemingly simple initial value problem: If too large a step size is used in an explicit method, this results in strongly oscillating values that build up over the course of the calculation and move further and further away from the exact solution. Implicit methods, on the other hand, typically calculate the solution for arbitrary step sizes qualitatively correctly, namely as an exponentially decreasing sequence of approximate values.

More generally, the above test equation is also considered for complex values of $\lambda$ . In this case, the solutions are oscillations whose amplitude remains limited precisely when $\operatorname {Re} (\lambda )\leq 0$, i.e. the real part of $\lambda$ is less than or equal to 0. This makes it possible to formulate a desirable property of one-step methods that are to be used for stiff initial value problems: the so-called A-stability. A method is called A-stable if it calculates a sequence of approximations $h>0$for any step size $y_{0},y_{1},y_{2},\dotsc$ applied to the test equation for all $\lambda$with $\operatorname {Re} (\lambda )\leq 0$, which remains bounded (like the true solution). The implicit Euler method and the implicit trapezoidal method are the simplest examples of A-stable one-step methods. On the other hand, it can be shown that an explicit method can never be A-stable.

Special procedures and procedure classes

Simple procedures of order 1 and 2

Einige Einschrittverfahren im Vergleich

As the French mathematician Augustin-Louis Cauchy proved around 1820, the Euler method has a convergence order of 1. If you average the slopes $f(t_{j},y_{j})$ of the explicit Euler method and $f(t_{j+1},y_{j+1})$ of the implicit Euler method, as they exist at the two end points of a step, you can hope to obtain a better approximation over the entire interval. In fact, it can be proven that the implicit trapezoidal method obtained in this way

$y_{j+1}=y_{j}+{\frac {h}{2}}{\Big (}f(t_{j},y_{j})+f(t_{j+1},y_{j+1}){\Big )}$

has a convergence order of 2. This method has very good stability properties, but is implicit, meaning that an equation for 𝑦 𝑗 + 1 must be solved in each step. If this variable is approximated on the right-hand side of the equation using the explicit Euler method, the result is the explicit method of Heun

$y_{j+1}=y_{j}+{\frac {h}{2}}{\Big (}f(t_{j},y_{j})+f{\big (}t_{j+1},y_{j}+hf(t_{j},y_{j}){\big )}{\Big )}$,

which also has convergence order 2. Another simple explicit method of order 2, the improved Euler method, is obtained by the following consideration: A "mean" slope in the method step would be the slope of the solution 𝑦 in the middle of the step, i.e. at the point $y_{j+1}$ . However, as the solution is unknown, it is approximated by an explicit Euler step with half the step size. This results in the following procedure

$y_{j+1}=y_{j}+hf{\big (}t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}f(t_{j},y_{j}){\big )}$.

These one-step methods of order 2 were all published as improvements of the Euler method in 1895 by the German mathematician Carl Runge.

Runge-Kutta method

Das klassische Runge-Kutta-Verfahren vierter Ordnung mittelt in jedem Schritt vier Hilfssteigungen (rot)

The aforementioned ideas for simple one-step methods lead to the important class of Runge-Kutta methods when generalized further. For example, Heun's method can be presented more clearly as follows: First, an auxiliary slope $k_{1}=f(t_{j},y_{j})$ is calculated, namely the slope of the explicit Euler method. This is used to determine a further auxiliary slope, here $k_{2}=f(t_{j}+h,y_{j}+hk_{1})$ . The actual process gradient $\Phi$ used is then calculated as a weighted average of the auxiliary gradients, i.e. ${\tfrac {1}{2}}k_{1}+{\tfrac {1}{2}}k_{2}$ in Heun's method. This procedure can be generalized to more than two auxiliary slopes. An $s$- -stage Runge-Kutta method first calculates auxiliary slopes $k_{1},\dotsc ,k_{s}$ by evaluating 𝑓 at suitable points and then $\Phi$ as a weighted average. In an explicit Runge-Kutta method, the auxiliary slopes $k_{1},k_{2},k_{3},\dotsc$are calculated directly one after the other; in an implicit method, they are obtained as solutions to a system of equations. A typical example is the explicit classical Runge-Kutta method of order 4, which is sometimes simply referred to as the Runge-Kutta method: First, the four auxiliary slopes

${\begin{aligned}k_{1}&=f(t_{j},y_{j})\\k_{2}&=f(t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}k_{1})\\k_{3}&=f(t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}k_{2})\\k_{4}&=f(t_{j}+h,y_{j}+hk_{3})\end{aligned}}$

and then the weighted average is calculated as the process slope

${\tfrac {1}{6}}k_{1}+{\tfrac {1}{3}}k_{2}+{\tfrac {1}{3}}k_{3}+{\tfrac {1}{6}}k_{4}$

is used. This well-known method was published by the German mathematician Wilhelm Kutta in 1901, after Karl Heun had found a three-step one-step method of order 3 a year earlier.

The construction of explicit methods of even higher order with the smallest possible number of steps is a mathematically quite demanding problem. As John C. Butcher was able to show in 1965, there are, for example, only a minimum of six steps for order 5; an explicit Runge-Kutta method of order 8 requires at least 11 steps. In 1978, the Austrian mathematician Ernst Hairer found a method of order 10 with 17 levels. The coefficients for such a method must fulfill 1205 determinant equations. With implicit Runge-Kutta methods, the situation is simpler and clearer: for every number of steps $s$ there is a method of order $p=2s$ ; this is also the maximum achievable order.

Extrapolation method

Extrapolation auf $h=0$ bei einem Verfahren der Ordnung ${\textstyle p=2}$

The idea of extrapolation is not limited to the solution of initial value problems with one-step methods, but can be applied analogously to all numerical methods that discretize the problem to be solved with a step size $h$. A well-known example of an extrapolation method is the Romberg integration for the numerical calculation of integrals. In general, let $v$ be a value that is to be determined numerically, in the case of this article, for example, the value of the solution function of an initial value problem at a given point. A numerical method, for example a one-step method, calculates an approximate value ${\tilde {v}}(h)$ for this, which depends on the choice of step size $h>0$. It is assumed that the method is convergent, i.e. that ${\tilde {v}}(h)$ converges to $v$ when $h$ converges to zero. However, this convergence is only a purely theoretical statement, as approximate values ${\tilde {v}}(h_{1}),{\tilde {v}}(h_{2}),\dotsc ,{\tilde {v}}(h_{m})$ can be calculated for a finite number of different step sizes $h_{1}>h_{2}>\ldots >h_{m}$ , but of course the step size cannot be allowed to "converge to zero". However, the calculated approximations for different step sizes can be interpreted as information about the (unknown) function ${\tilde {v}}$: In the extrapolation methods, ${\tilde {v}}$ is approximated by an interpolation polynomial, i.e. by a polynomial $P$ with

$P(h_{k})={\tilde {v}}(h_{k})$

for $k=1,2,\dotsc ,m$ . The value $P(0)$ of the polynomial at the point $h=0$ is then used as a computable approximation for the non-computable limit value of ${\tilde {v}}(h)$ for $h$ towards zero. An early successful extrapolation algorithm for initial value problems was published by Roland Bulirsch and Josef Stoer in 1966.

A concrete example in the case of a one-step method of order $p$ can illustrate the general procedure of extrapolation. With such a method, the calculated approximation for small step sizes ℎ can be easily described by a polynomial of the form

$P(h)=a+bh^{p}$

with initially unknown parameters $a$ and $b$. If you now calculate two approximations $y_{h_{1}}$ and $y_{h_{2}}$ using the method for a step size $h_{1}$ and for half the step size $h_{2}={\tfrac {1}{2}}h_{1}$, two linear equations for the unknowns $a$ and $b$ are obtained from the interpolation conditions $P(h_{1})=y_{h_{1}}$ and $P(h_{2})=y_{h_{2}}$.

The value extrapolated to 

$P(0)=a=y_{h_{2}}+{\frac {y_{h_{2}}-y_{h_{1}}}{2^{p}-1}}$

is then generally a significantly better approximation than the two values calculated initially. It can be shown that the order of the one-step method obtained in this way is at least $p+1$, i.e. at least 1 greater than the original method.

Method with step width control

One advantage of the one-step method is that any step size $j$ can be used in each step 𝑗 independently of the other steps. In practice, this obviously raises the question of how ℎ 𝑗 should be selected. In real applications, there will always be an error tolerance with which the solution of an initial value problem is to be calculated; for example, it would be pointless to determine a numerical approximation that is significantly more "accurate" than the data for initial values and parameters of the given problem, which are subject to measurement errors. The aim will therefore be to select the step sizes in such a way that, on the one hand, the specified error tolerances are adhered to and, on the other hand, as few steps as possible are used in order to keep the computational effort to a minimum. This problem, in which an ordinary differential equation is given together with an initial condition, plays a central role in all natural and engineering sciences and is also becoming increasingly important in the economic and social sciences, for example. Initial value problems are used to analyze, simulate or predict dynamic processes.

For well-conditioned initial value problems, it can be shown that the global process error is approximately equal to the sum of the local truncation errors $\eta _{j}:=\|\eta (t_{j},h_{j})\|$ in the individual steps. Therefore, the largest possible $h_{j}$ should be selected as the step size, for which $\eta _{j}$ is below a selected tolerance threshold. The problem here is that $\eta _{j}$ cannot be calculated directly, as it depends on the unknown exact solution $y(t_{j})$ of the initial value problem at the point $t_{j}$. The basic idea of step size control is therefore to approximate $y(t_{j})$ with a method that is more accurate than the underlying basic method.

Two basic ideas for step width control are step width halving and embedded processes. With step size halving, the result for two steps with half the step size is calculated as a comparison value in addition to the actual process step. A more precise approximation for $y(t_{j})$ is then determined from both values by extrapolation and the local error 𝜂 𝑗 is estimated. If this is too large, this step is discarded and repeated with a smaller step size. If it is significantly smaller than the specified tolerance, the step size can be increased in the next step. The additional computational effort for this step width halving procedure is relatively high; this is why modern implementations usually use so-called embedded procedures for step width control. The basic idea is to calculate two approximations for $y(t_{j})$ in each step using two one-step methods that have different orders of convergence and thus estimate the local error. In order to optimize the computational effort, the two methods should have as many computational steps in common as possible: They should be "embedded in each other". Embedded Runge-Kutta methods, for example, use the same auxiliary slopes and differ only in how they average them. Well-known embedded methods include the Runge-Kutta-Fehlberg method (Erwin Fehlberg, 1969) and the Dormand-Prince method (J. R. Dormand and P. J. Prince, 1980).

Practical example: Solving initial value problems with numerical software

Numerous software implementations have been developed for the mathematical concepts outlined in this article, which allow the user to solve practical problems numerically in a simple way. As a concrete example, a solution to the Lotka-Volterra equations will now be calculated using the popular numerical software Matlab. The Lotka-Volterra equations are a simple model from biology that describes the interactions between predator and prey populations. Given the differential equation system

${\begin{aligned}y_{1}'(t)&=ay_{1}(t)-by_{1}(t)y_{2}(t)\\y_{2}'(t)&=cy_{1}(t)y_{2}(t)-dy_{2}(t)\end{aligned}}$

with the parameters $a=1,b=2,c=1,d=1$ and the initial condition $y_{1}(0)=3$, $y_{2}(0)=1$. Here, $y_{1}$ and $y_{2}$ correspond to the temporal development of the prey and predator population respectively. The solution should be calculated on the time interval $[0,20]$.

For the calculation using Matlab, the function $f$ is first defined for the given parameter values on the right-hand side of the differential equation $y'=f(t,y)$:

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

The time interval and the initial values are also required:

t_int = [0, 20];
y0 = [3; 1];

The solution can then be calculated:

[t, y] = ode45(f, t_int, y0);

The Matlab function ode45 implements a one-step method that uses two embedded explicit Runge-Kutta methods with convergence orders 4 and 5 for step size control.

The solution can now be plotted, $y_{1}$ as a blue curve and $y_{2}$ as a red curve; the calculated points are marked by small circles:

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

The result is shown below in the left-hand image. The right-hand image shows the step sizes used by the method and was generated with

figure(2)
plot(t(1:end-1), diff(t))

This example can also be executed without changes using the free numerical software GNU Octave. However, the method implemented there results in a slightly different step size sequence.

Literature

• John C. Butcher (2008), Numerical Methods for Ordinary Differential Equations, Chichester: John Wiley & Sons, ISBN 978-0-470-72335-7
• Wolfgang Dahmen, Arnold Reusken (2008), "Kap. 11: Gewöhnliche Differentialgleichungen", Numerik für Ingenieure und Naturwissenschaftler (2. ed.), Berlin/Heidelberg: Springer, ISBN 978-3-540-76492-2
• Peter Deuflhard, Folkmar Bornemann (2008), Numerische Mathematik 2 – Gewöhnliche Differentialgleichungen (3. ed.), Berlin: Walter de Gruyter, ISBN 978-3-11-020356-1
• David F. Griffiths, Desmond J. Higham (2010), Numerical Methods for Ordinary Differential Equations – Initial Value Problems, London: Springer, ISBN 978-0-85729-147-9
• Robert Plato (2010), "Kap. 7: Einschrittverfahren für Anfangswertprobleme", Numerische Mathematik kompakt (4. ed.), Wiesbaden: Vieweg+Teubner, ISBN 978-3-8348-1018-2
• Hans-Jürgen Reinhardt (2012), Numerik gewöhnlicher Differentialgleichungen (2. ed.), Berlin/Boston: Walter de Gruyter, ISBN 978-3-11-028045-6
• Hans Rudolf Schwarz, Norbert Köckler (2011), "Kap. 8: Anfangswertprobleme", Numerische Mathematik (8. ed.), Wiesbaden: Vieweg+Teubner, ISBN 978-3-8348-1551-4
• Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky (2012), Numerik gewöhnlicher Differentialgleichungen (2. ed.), Wiesbaden: Springer Spektrum, ISBN 978-3-8348-1847-8{{citation}}: CS1 maint: multiple names: authors list (link)

External links

• Lars Grüne (2008). "Numerical Methods for Ordinary Differential Equations (Numerical Mathematics II)" (PDF). Retrieved 2018-08-20.
• Peter Spellucci (2007). "Numerik gewöhnlicher Differentialgleichungen" (PDF). Retrieved 2018-08-20.
• Hans U. Fuchs (2007). "Numerical Methods for Differential Equations" (PDF). Retrieved 2018-08-20.
• "Mathe Tutorial: Rechner für allgemeine Differentialgleichungen 1. Ordnung". Mathe Tutorial. Retrieved 2018-08-20.

References

This page will be placed in the following categories if it is moved to the article namespace.

Categories:

• Computational mathematics
• Differential equations