List of regular polytope compounds
This article lists the regular polytope compounds in Euclidean, spherical and hyperbolic spaces.
Two dimensional compounds[edit]
For any natural number n, there are n-pointed star regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime. When m and n are not coprime, the star polygon obtained will be a regular polygon with n/m sides. A new figure is obtained by rotating these regular n/m-gons one vertex to the left on the original polygon until the number of vertices rotated equals n/m minus one, and combining these figures. An extreme case of this is where n/m is 2, producing a figure consisting of n/2 straight line segments; this is called a degenerate star polygon.
In other cases where n and m have a common factor, a star polygon for a lower n is obtained, and rotated versions can be combined. These figures are called star figures, improper star polygons or compound polygons. The same notation {n/m} is often used for them, although authorities such as Grünbaum (1994) regard (with some justification) the form k{n} as being more correct, where usually k = m.
A further complication comes when we compound two or more star polygons, as for example two pentagrams, differing by a rotation of 36°, inscribed in a decagon. This is correctly written in the form k{n/m}, as 2{5/2}, rather than the commonly used {10/4}.
Coxeter's extended notation for compounds is of the form c{m,n,...}[d{p,q,...}]e{s,t,...}, indicating that d distinct {p,q,...}'s together cover the vertices of {m,n,...} c times and the facets of {s,t,...} e times. If no regular {m,n,...} exists, the first part of the notation is removed, leaving [d{p,q,...}]e{s,t,...}; the opposite holds if no regular {s,t,...} exists. The dual of c{m,n,...}[d{p,q,...}]e{s,t,...} is e{t,s,...}[d{q,p,...}]c{n,m,...}. If c or e are 1, they may be omitted. For compound polygons, this notation reduces to {nk}[k{n/m}]{nk}: for example, the hexagram may be written thus as {6}[2{3}]{6}.
 2{2} |
3{2} |
 4{2} |
5{2} |
 6{2} |
7{2} |
 8{2} |
9{2} |
 10{2} |
 11{2} |
 12{2} |
 13{2} |
 14{2} |
 15{2} | |
2{3} |
 3{3} |
 4{3} |
 5{3} |
6{3} |
 7{3} |
 8{3} |
 9{3} |
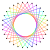 10{3} |
 2{4} |
 3{4} |
 4{4} |
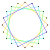 5{4} |
 6{4} |
 7{4} |
2{5} |
 3{5} |
 4{5} |
 5{5} |
 6{5} |
2{5/2} |
 3{5/2} |
 4{5/2} |
 5{5/2} |
 6{5/2} |
 2{6} |
3{6} |
 4{6} |
 5{6} | |
2{7} |
 3{7} |
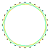 4{7} |
2{7/2} |
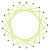 3{7/2} |
 4{7/2} |
2{7/3} |
 3{7/3} |
 4{7/3} |
 2{8} |
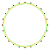 3{8} |
 2{8/3} |
 3{8/3} | ||
2{9} |
 3{9} |
2{9/2} |
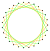 3{9/2} |
2{9/4} |
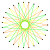 3{9/4} |
 2{10} |
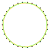 3{10} |
 2{10/3} |
 3{10/3} | |||||
 2{11} |
 2{11/2} |
 2{11/3} |
 2{11/4} |
 2{11/5} |
 2{12} |
 2{12/5} |
 2{13} |
 2{13/2} |
 2{13/3} |
 2{13/4} |
 2{13/5} |
 2{13/6} | ||
 2{14} |
 2{14/3} |
 2{14/5} |
 2{15} |
 2{15/2} |
 2{15/4} |
 2{15/7} |
Regular skew polygons also create compounds, seen in the edges of prismatic compound of antiprisms, for instance:
| Compound skew squares |
Compound skew hexagons |
Compound skew decagons | |
| Two {2}#{ } | Three {2}#{ } | Two {3}#{ } | Two {5/3}#{ } |

|

|
|

|
Three dimensional compounds[edit]
This section's factual accuracy is disputed. (January 2024) |
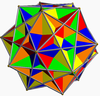
A regular polyhedron compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. With this definition there are 5 regular compounds.
| Symmetry | [4,3], Oh | [5,3]+, I | [5,3], Ih | ||
|---|---|---|---|---|---|
| Duality | Self-dual | Dual pairs | |||
| Image | 
|

|

|
|

|
| Spherical | 
|

|

|

|

|
| Polyhedra | 2 {3,3} | 5 {3,3} | 10 {3,3} | 5 {4,3} | 5 {3,4} |
| Coxeter | {4,3}[2{3,3}]{3,4} | {5,3}[5{3,3}]{3,5} | 2{5,3}[10{3,3}]2{3,5} | 2{5,3}[5{4,3}] | [5{3,4}]2{3,5} |
Coxeter's notation for regular compounds is given in the table above, incorporating Schläfli symbols. The material inside the square brackets, [d{p,q}], denotes the components of the compound: d separate {p,q}'s. The material before the square brackets denotes the vertex arrangement of the compound: c{m,n}[d{p,q}] is a compound of d {p,q}'s sharing the vertices of an {m,n} counted c times. The material after the square brackets denotes the facet arrangement of the compound: [d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the faces of {s,t} counted e times. These may be combined: thus c{m,n}[d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the vertices of {m,n} counted c times and the faces of {s,t} counted e times. This notation can be generalised to compounds in any number of dimensions.[1]
Euclidean and hyperbolic plane compounds[edit]
There are eighteen two-parameter families of regular compound tessellations of the Euclidean plane. In the hyperbolic plane, five one-parameter families and seventeen isolated cases are known, but the completeness of this listing has not yet been proven.
The Euclidean and hyperbolic compound families 2 {p,p} (4 ≤ p ≤ ∞, p an integer) are analogous to the spherical stella octangula, 2 {3,3}.
| Self-dual | Duals | Self-dual | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞,∞} |

|

|

|

|
| {{4,4}} or a{4,4} or {4,4}[2{4,4}]{4,4} |
[2{6,3}]{3,6} | a{6,3} or {6,3}[2{3,6}] |
{{∞,∞}} or a{∞,∞} or {4,∞}[2{∞,∞}]{∞,4} |
| 3 {6,3} | 3 {3,6} | 3 {∞,∞} | |

|

|

| |
| 2{3,6}[3{6,3}]{6,3} | {3,6}[3{3,6}]2{6,3} |
||
Four dimensional compounds[edit]

|

|
| 75 {4,3,3} | 75 {3,3,4} |
|---|
Coxeter lists 32 regular compounds of regular 4-polytopes in his book Regular Polytopes.[2] McMullen adds six in his paper New Regular Compounds of 4-Polytopes, in which he also proves that the list is now complete.[3] In the following tables, the superscript (var) indicates that the labeled compounds are distinct from the other compounds with the same symbols.
| Compound | Constituent | Symmetry | Vertex arrangement | Cell arrangement |
|---|---|---|---|---|
| 120 {3,3,3} | 5-cell | [5,3,3], order 14400[2] | {5,3,3} | {3,3,5} |
| 120 {3,3,3}(var) | 5-cell | order 1200[3] | {5,3,3} | {3,3,5} |
| 720 {3,3,3} | 5-cell | [5,3,3], order 14400[3] | 6{5,3,3} | 6{3,3,5} |
| 5 {3,4,3} | 24-cell | [5,3,3], order 14400[2] | {3,3,5} | {5,3,3} |
| Compound 1 | Compound 2 | Symmetry | Vertex arrangement (1) | Cell arrangement (1) | Vertex arrangement (2) | Cell arrangement (2) |
|---|---|---|---|---|---|---|
| 3 {3,3,4}[4] | 3 {4,3,3} | [3,4,3], order 1152[2] | {3,4,3} | 2{3,4,3} | 2{3,4,3} | {3,4,3} |
| 15 {3,3,4} | 15 {4,3,3} | [5,3,3], order 14400[2] | {3,3,5} | 2{5,3,3} | 2{3,3,5} | {5,3,3} |
| 75 {3,3,4} | 75 {4,3,3} | [5,3,3], order 14400[2] | 5{3,3,5} | 10{5,3,3} | 10{3,3,5} | 5{5,3,3} |
| 75 {3,3,4} | 75 {4,3,3} | [5,3,3], order 14400[2] | {5,3,3} | 2{3,3,5} | 2{5,3,3} | {3,3,5} |
| 75 {3,3,4} | 75 {4,3,3} | order 600[3] | {5,3,3} | 2{3,3,5} | 2{5,3,3} | {3,3,5} |
| 300 {3,3,4} | 300 {4,3,3} | [5,3,3]+, order 7200[2] | 4{5,3,3} | 8{3,3,5} | 8{5,3,3} | 4{3,3,5} |
| 600 {3,3,4} | 600 {4,3,3} | [5,3,3], order 14400[2] | 8{5,3,3} | 16{3,3,5} | 16{5,3,3} | 8{3,3,5} |
| 25 {3,4,3} | 25 {3,4,3} | [5,3,3], order 14400[2] | {5,3,3} | 5{5,3,3} | 5{3,3,5} | {3,3,5} |
There are two different compounds of 75 tesseracts: one shares the vertices of a 120-cell, while the other shares the vertices of a 600-cell. It immediately follows therefore that the corresponding dual compounds of 75 16-cells are also different.
| Compound | Symmetry | Vertex arrangement | Cell arrangement |
|---|---|---|---|
| 5 {5,5/2,5} | [5,3,3]+, order 7200[2] | {5,3,3} | {3,3,5} |
| 10 {5,5/2,5} | [5,3,3], order 14400[2] | 2{5,3,3} | 2{3,3,5} |
| 5 {5/2,5,5/2} | [5,3,3]+, order 7200[2] | {5,3,3} | {3,3,5} |
| 10 {5/2,5,5/2} | [5,3,3], order 14400[2] | 2{5,3,3} | 2{3,3,5} |
| Compound 1 | Compound 2 | Symmetry | Vertex arrangement (1) | Cell arrangement (1) | Vertex arrangement (2) | Cell arrangement (2) |
|---|---|---|---|---|---|---|
| 5 {3,5,5/2} | 5 {5/2,5,3} | [5,3,3]+, order 7200[2] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], order 14400[2] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3]+, order 7200[2] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], order 14400[2] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
| 5 {5/2,3,5} | 5 {5,3,5/2} | [5,3,3]+, order 7200[2] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], order 14400[2] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
There are also fourteen partially regular compounds, that are either vertex-transitive or cell-transitive but not both. The seven vertex-transitive partially regular compounds are the duals of the seven cell-transitive partially regular compounds.
| Compound 1 Vertex-transitive |
Compound 2 Cell-transitive |
Symmetry |
|---|---|---|
| 2 16-cells[5] | 2 tesseracts | [4,3,3], order 384[2] |
| 25 24-cell(var) | 25 24-cell(var) | order 600[3] |
| 100 24-cell | 100 24-cell | [5,3,3]+, order 7200[2] |
| 200 24-cell | 200 24-cell | [5,3,3], order 14400[2] |
| 5 600-cell | 5 120-cell | [5,3,3]+, order 7200[2] |
| 10 600-cell | 10 120-cell | [5,3,3], order 14400[2] |
| Compound 1 Vertex-transitive |
Compound 2 Cell-transitive |
Symmetry |
|---|---|---|
| 5 {3,3,5/2} | 5 {5/2,3,3} | [5,3,3]+, order 7200[2] |
| 10 {3,3,5/2} | 10 {5/2,3,3} | [5,3,3], order 14400[2] |
Although the 5-cell and 24-cell are both self-dual, their dual compounds (the compound of two 5-cells and compound of two 24-cells) are not considered to be regular, unlike the compound of two tetrahedra and the various dual polygon compounds, because they are neither vertex-regular nor cell-regular: they are not facetings or stellations of any regular 4-polytope. However, they are vertex-, edge-, face-, and cell-transitive.
Euclidean 3-space compounds[edit]
The only regular Euclidean compound honeycombs are an infinite family of compounds of cubic honeycombs, all sharing vertices and faces with another cubic honeycomb. This compound can have any number of cubic honeycombs. The Coxeter notation is {4,3,4}[d{4,3,4}]{4,3,4}.
Five dimensions and higher compounds[edit]
There are no regular compounds in five or six dimensions. There are three known seven-dimensional compounds (16, 240, or 480 7-simplices), and six known eight-dimensional ones (16, 240, or 480 8-cubes or 8-orthoplexes). There is also one compound of n-simplices in n-dimensional space provided that n is one less than a power of two, and also two compounds (one of n-cubes and a dual one of n-orthoplexes) in n-dimensional space if n is a power of two.
The Coxeter notation for these compounds are (using αn = {3n−1}, βn = {3n−2,4}, γn = {4,3n−2}):
- 7-simplexes: cγ7[16cα7]cβ7, where c = 1, 15, or 30
- 8-orthoplexes: cγ8[16cβ8]
- 8-cubes: [16cγ8]cβ8
The general cases (where n = 2k and d = 22k − k − 1, k = 2, 3, 4, ...):
- Simplexes: γn−1[dαn−1]βn−1
- Orthoplexes: γn[dβn]
- Hypercubes: [dγn]βn
Euclidean honeycomb compounds[edit]
A known family of regular Euclidean compound honeycombs in five or more dimensions is an infinite family of compounds of hypercubic honeycombs, all sharing vertices and faces with another hypercubic honeycomb. This compound can have any number of hypercubic honeycombs. The Coxeter notation is δn[dδn]δn where δn = {∞} when n = 2 and {4,3n−3,4} when n ≥ 3.
References[edit]
Bibliography[edit]
- Coxeter, H. S. M. (1973) [1948]. Regular Polytopes (Third ed.). New York: Dover Publications. ISBN 0-486-61480-8. MR 0370327. OCLC 798003. See in particular Tables I and II: Regular polytopes and honeycombs, pp. 294–296.
- McMullen, Peter (2018), "New Regular Compounds of 4-Polytopes", New Trends in Intuitive Geometry, Bolyai Society Mathematical Studies, vol. 27, pp. 307–320, doi:10.1007/978-3-662-57413-3_12, ISBN 978-3-662-57412-6.
