Spiral similarity

A spiral similarity taking triangle ABC to triangle A'B'C'.

Spiral similarity is a plane transformation in mathematics composed of a rotation and a dilation. It is used widely in Euclidean geometry to facilitate the proofs of many theorems and other results in geometry, especially in mathematical competitions and olympiads. Though the origin of this idea is not known, it was documented in 1967 by Coxeter in his book Geometry Revisited. and 1969 - using the term "dilative rotation" - in his book Introduction to Geometry.

The following theorem is important for the Euclidean plane:
Any two directly similar figures are related either by a translation or by a spiral similarity.
(Hint: Directly similar figures are similar and have the same orientation)

Definition

A spiral similarity $S$ is composed of a rotation of the plane followed a dilation about a center $O$ with coordinates $c$ in the plane. Expressing the rotation by a linear transformation $T(x)$ and the dilation as multiplying by a scale factor $d$, a point $p$ gets mapped to

$$S(p)=d(T(p-c))+c.$$

On the complex plane, any spiral similarity can be expressed in the form $T(x)=x_{0}+\alpha (x-x_{0})$, where $\alpha$ is a complex number. The magnitude $|\alpha |$ is the dilation factor of the spiral similarity, and the argument ${\text{arg}}(\alpha )$ is the angle of rotation.

Properties

Two circles

Spiral similarity

Let T be a spiral similarity mapping circle k to k' with k $\cap$ k' = {C, D} and fixed point C.

Then for each point P $\in$ k the points P, T(P)= P' and D are collinear.

Remark: This property is the basis for the construction of the center of a spiral similarity for two linesegments.

Proof:

$\angle CMP=\angle CM'P'$, as rotation and dilation preserve angles.

$\angle P'DC+\angle CDP=180^{\circ }$, as if the radius ${\overline {MD}}$ intersects the chord ${\overline {CP}}$ , then ${\overline {M'D}}$ doesn't meet ${\overline {CP'}}$ , and if ${\overline {MD}}$ doesn't intersect ${\overline {CP}}$, then ${\overline {M'D}}$ intersects ${\overline {CP'}}$, so one of these angles is $\beta$ and the other is $180^{\circ }-\beta$.

So P, P' and D are collinear.

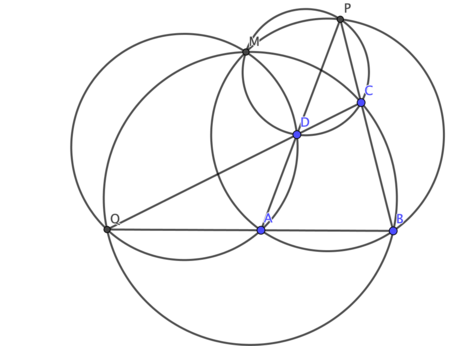
Center of a spiral similarity for two line segments

Through a dilation of a line, rotation, and translation, any line segment can be mapped into any other through the series of plane transformations. We can find the center of the spiral similarity through the following construction:

• Draw lines ${\overline {AC}}$ and ${\overline {BD}}$, and let $P$ be the intersection of the two lines.
• Draw the circumcircles of triangles $\triangle PAB$ and $\triangle PCD$.
• The circumcircles intersect at a second point $X\neq P$. Then $X$ is the spiral center mapping ${\overline {AB}}$ to ${\overline {CD}}.$

Proof: Note that $ABPX$ and $XPCD$ are cyclic quadrilaterals. Thus, $\angle XAB=180^{\circ }-\angle BPX=\angle XPD=\angle XCD$. Similarly, $\angle ABX=\angle APX=180^{\circ }-\angle XPC=\angle XDC$. Therefore, by AA similarity, triangles $XAB$ and $XCD$ are similar. Thus, $\angle AXB=\angle CXD,$ so a rotation angle mapping $A$ to $B$ also maps $C$ to $D$. The dilation factor is then just the ratio of side lengths ${\overline {CD}}$ to ${\overline {AB}}$.

Solution with complex numbers

If we express $A,B,C,$ and $D$ as points on the complex plane with corresponding complex numbers $a,b,c,$ and $d$, we can solve for the expression of the spiral similarity which takes $A$ to $C$ and $B$ to $D$. Note that $T(a)=x_{0}+\alpha (a-x_{0})$ and $T(b)=x_{0}+\alpha (b-x_{0})$, so ${\frac {T(b)-T(a)}{b-a}}=\alpha$. Since $T(a)=c$ and $T(b)=d$, we plug in to obtain $\alpha ={\frac {d-c}{b-a}}$, from which we obtain $x_{0}={\frac {ad-bc}{a+d-b-c}}$.

Pairs of spiral similarities

For any points $A,B,C,$ and $D$, the center of the spiral similarity taking ${\overline {AB}}$ to ${\overline {CD}}$ is also the center of a spiral similarity taking ${\overline {AC}}$ to ${\overline {BD}}$.

This can be seen through the above construction. If we let $X$ be the center of spiral similarity taking ${\overline {AB}}$ to ${\overline {CD}}$, then $\triangle XAB\sim \triangle XCD$. Therefore, $\angle AXC=\angle AXB+\angle BXC=\angle CXD+\angle BXC=\angle BXD$. Also, ${\frac {AX}{BX}}={\frac {CX}{DX}}$ implies that ${\frac {AX}{CX}}={\frac {BX}{DX}}$. So, by SAS similarity, we see that $\triangle AXC\sim \triangle BXD$. Thus $X$ is also the center of the spiral similarity which takes ${\overline {AC}}$ to ${\overline {BD}}$.

Corollaries

Proof of Miquel's Quadrilateral Theorem

Spiral similarity can be used to prove Miquel's Quadrilateral Theorem: given four noncollinear points $A,B,C,$ and $D$, the circumcircles of the four triangles $\triangle PAB,\triangle PDC,\triangle QAD,$ and $\triangle QBC$ intersect at one point, where $P$ is the intersection of $AD$ and $BC$ and $Q$ is the intersection of $AB$ and $CD$ (see diagram).

Let $M$ be the center of the spiral similarity which takes $AB$ to $DC$. By the above construction, the circumcircles of $\triangle PAB$ and $\triangle PDC$ intersect at $M$ and $P$. Since $M$ is also the center of the spiral similarity taking $DA$ to $BC$, by similar reasoning the circumcircles of $\triangle QAD$ and $\triangle QBC$ meet at $Q$ and $M$. Thus, all four circles intersect at $M$.

Example problem

Here is an example problem on the 2018 Japan MO Finals which can be solved using spiral similarity:

Given a scalene triangle $ABC$, let $D$ and $E$ be points on segments $AB$ and $AC$, respectively, so that $CA=CD,BA=BE$. Let $\omega$ be the circumcircle of triangle $ADE$ and $P$ the reflection of $A$ across $BC$. Lines $PD$ and $PE$ meet $\omega$ again at $X$ and $Y$, respectively. Prove that $BX$ and $CY$ intersect on $\omega$.

Proof: We first prove the following claims:

Claim 1: Quadrilateral $PBEC$ is cyclic.

Proof: Since $\triangle BAE$ is isosceles, we note that $\angle BPC=\angle BAC=180^{\circ }-\angle BEC,$ thus proving that quadrilateral $PBEC$ is cyclic, as desired. By symmetry, we can prove that quadrilateral $PBDC$ is cyclic.

Claim 2: $\triangle AXY\sim \triangle ABC.$

Proof: We have that $\angle AXY=180^{\circ }-\angle AEY=\angle YEC=\angle PEC=\angle PBC=\angle ABC.$ By similar reasoning, $\angle AYX=\angle ACB,$ so by AA similarity, $\triangle AXY\sim \triangle ABC,$ as desired.

We now note that $A$ is the spiral center that maps $XY$ to $BC$. Let $F$ be the intersection of $BX$ and $CY$. By the spiral similarity construction above, the spiral center must be the intersection of the circumcircles of $\triangle FXY$ and $\triangle FBC$. However, this point is $A$, so thus points $A,F,X,Y$ must be concyclic. Hence, $F$ must lie on $\omega$, as desired.