Talk:Exponential object
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
Is Y or Z required to be locally compact Hausdorff?
[edit]The text currently seems to confuse Y and Z. Can someone with the knowledge fix it? It looks like a misprint, but I don't want to correct it without being 100% sure.--345Kai 19:22, 2 March 2007 (UTC)
- No, its stated correctly, Y must be locally compact. In particular, if Y is locally compact, then the evaluation map is continuous. See compact-open topology. -- Fropuff 20:05, 2 March 2007 (UTC)
- Maybe I should have been more specific where I fear the misprit is. I've highlited it in the corresponding paragraph:
- In the category of topological spaces, the exponential object ZY exists provided that Y is a locally compact Hausdorff space. In that case, the space ZY is the set of all continuous functions from Y to Z together with the compact-open topology. The evaluation map is the same as in the category of sets. If Y is not locally compact Hausdorff, the exponential object may not exist (the space ZY exists, but fails to be an exponential object because the adjunction with the product only holds when is locally compact Hausdorff). For this reason the category of topological spaces fails to be cartesian closed.
- Should the "big Z" be a Y? Thanks for the help! --345Kai 15:06, 4 March 2007 (UTC)
- Oh right, thanks. I've fixed it now. -- Fropuff 16:32, 4 March 2007 (UTC)
notational difficulties
[edit]I just tripped over this article, and am having several notational struggles. One is with the lambda: the convention I'm used to, for currying, is that if
then
This makes it clear that y is the free variable, whereas implies that g is free, which its not.
The other confusion is the yin and yang of eval/apply. This article says eval, whereas its clear that apply was meant. I just wrote the article on apply earlier today, trying to give a somewhat-clear if rather lazy catagory theoretic definition of it. After reading this article, I notice that there is more than a little collision, and I can't resolve it off the top of my head.
In particular, the diagram
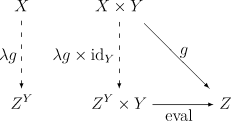
is essentially identical to
except that I don't have diagram-drawing software, and that what this article calls I called curry(g), and what this article calls "eval" should really be called "apply".
The final problem is that, perhaps, the apply article uses Hom whereas I'm thinking that correctly, perhaps it should have used the exponential object. I'm confused about that. Sigh. linas (talk) 07:02, 23 November 2007 (UTC)
- Hello. eval is very common notation for that arrow (see eg Mac Lane), but you are right, it has nothing to do with the meaning described on eval and more to do with apply. "eval" is used because the map evaluates the function at its argument. The lambda notation is also quite common for that arrow, although computer scientists might call it curry. The notation in this article should not be switched, because it is quite standard. However, there is already a link to the curry article, and a link should perhaps be included to your apply article.
- As regards the notation for the exponential: Hom(X,Y) usually describes the set of morphisms, and as such it is not an object of the category and so Hom(X,Y)x X makes no sense. Sometimes people talk about YX as an "internal hom" (most often with monoidal closed categories, though). Other people sometimes use notation , which might be more palatable in computer science. Sam Staton (talk) 10:28, 23 November 2007 (UTC)
- Hi Sam, you are right about Hom, I will fix that when I get a moment of clear-headedness. In my copious spare time :-), I'll modify the apply article to review some popular alternate notations. I suppose I should someday actually read Maclane instead of vaguely pretending I know what its about. Thanks.
- Oh, BTW, the article on currying has a particularly elegent and succinct paragraph describing the connection to Cartesian closed categories. I would very much like to see that paragraph copied to several related articles, as it captures (for me) the essence of the thing. I did not want to copy it myself, as I didn't want to propagate any subtle errors it might have, but perhaps ... could you review it for correctness? linas (talk) 04:02, 24 November 2007 (UTC)
- Hello linas, thanks for the paragraph clarifying the eval and apply terminology. I hope you don't mind, I abbreviated it a little. The notational connection with semantics of lambda calculus is closer than you seem to realize. If you have a term t:Z with free variables x:X, y;Y, the semantics is a morphism X x Y -> Z, giving a value in Z for every possible valuation of x, y. The term λy.t has one free variable, x, and its semantics is the morphism X -> ZY, found by currying. So the semantics of λ-abstraction is the same thing as currying. Hope that's clear. Perhaps all this should be explained in the article.
- Which paragraph of the currying article were you especially keen on? All the best, Sam Staton (talk) 15:36, 25 November 2007 (UTC)
No definition of power object
[edit]This article directs me to Topos for definition, but 'Topos' does not contain definition either. --Beroal (talk) 21:55, 24 September 2008 (UTC)
Exponential objects in the category of vector spaces?
[edit]While there is obviously a vector space of linear maps, it seems to me that it is not an exponential object in the category of vector spaces, since the evaluation map is not linear and therefore not a morphism in the category. Is this a mistake in the article or am I misunderstanding something? Tejing (talk) 19:33, 13 December 2016 (UTC)
- It isn't. See nLab: "An exponential object X^Y is an internal hom [Y,X] in a cartesian closed category." There holds the adjunction from the article. In the case of the abelian category of vector spcaes, this cannot hold. See explicitly in https://en.wikipedia.org/wiki/Cartesian_closed_category:
- A category with a zero object is Cartesian closed if and only if it is equivalent to a category with only one object and one identity morphism. Indeed, if 0 is an initial object and 1 is a final object and we have , then which has only one element.[1]
- In particular, any non-trivial category with a zero object, such as an abelian category, is not Cartesian closed. So the category of modules over a ring is not Cartesian closed. However, the functor tensor product with a fixed module does have a right adjoint. The tensor product is not a categorical product, so this does not contradict the above. We obtain instead that the category of modules is monoidal closed.
Julian Bitterwolf (talk) 20:48, 21 February 2017 (UTC)
References
I don't think "power object" should redirect here
[edit]A power object is a totally different notion (cf. https://ncatlab.org/nlab/show/power+object) generalizing the notion of a powerset from set theory, and one in general should not use the term "power object" to refer to exponential objects. There is a definition of it buried halfway through the definition of a topos at Topos#Formal_definition, but it deserves its own page, as the definition only requires a category with finite limits and doesn't really depend on all the other details of what a topos is.
Cgibbard (talk) 15:49, 1 November 2023 (UTC)
- I redirected power object to Topos#power object. -- Ancheta Wis (talk | contribs) 14:13, 2 November 2023 (UTC)








![{\displaystyle [X\Rightarrow Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55ce6d8084e2900230f5f18842c090ab6f8944fb)



