Trojan wave packet

Trojan wavepacket evolution animation

Classical simulation of the Trojan wavepacket on 1982 home ZX Spectrum microcomputer. The packet is approximated by the ensemble of points initially randomly localized within the peak of a Gaussian and moving according to the Newton equations. The ensemble stays localized. For the comparison the second simulation follows when the strength of the circularly polarized electric (rotating) field is equal to zero and the packet (points) fully spreads around the circle.

A trojan wave packet is a wave packet that is nonstationary and nonspreading. It is part of an artificially created system that consists of a nucleus and one or more electron wave packets, and that is highly excited under a continuous electromagnetic field. Its discovery as one of significant contributions to the Quantum Theory was awarded the 2022 Wigner Medal for Iwo Bialynicki-Birula

The strong, polarized electromagnetic field, holds or "traps" each electron wave packet in an intentionally selected orbit (energy shell). They derive their names from the trojan asteroids in the Sun–Jupiter system. Trojan asteroids orbit around the Sun in Jupiter's orbit at its Lagrangian equilibrium points L4 and L5, where they are phase-locked and protected from collision with each other, and this phenomenon is analogous to the way the wave packet is held together.

Concepts and research

The concept of the Trojan wave packet is derived from a flourishing area of physics which manipulates atoms and ions at the atomic level creating ion traps. Ion traps allow the manipulation of atoms and are used to create new states of matter including ionic liquids, Wigner crystals and Bose–Einstein condensates. This ability to manipulate the quantum properties directly is key to the development of applicable nanodevices such as quantum dots and microchip traps. In 2004 it was shown that it is possible to create a trap which is actually a single atom. Within the atom, the behavior of an electron can be manipulated.

During experiments in 2004 using lithium atoms in an excited state, researchers were able to localize an electron in a classical orbit for 15,000 orbits (900 ns). It was neither spreading nor dispersing. This "classical atom" was synthesized by "tethering" the electron using a microwave field to which its motion is phase locked. The phase lock of the electrons in this unique atomic system is, as mentioned above, analogous to the phase locked asteroids of Jupiter's orbit.

The techniques explored in this experiment are a solution to a problem that dates back to 1926. Physicists at that time realized that any initially localized wave packet will inevitably spread around the orbit of the electrons. Physicists noticed that "the wave equation is dispersive for the atomic Coulomb potential." In the 1980s several groups of researchers proved this to be true. The wave packets spread all the way around the orbits and coherently interfered with themselves. Recently the real world innovation realized with experiments such as Trojan wave packets, is localizing the wave packets, i.e., with no dispersion. Applying a polarized circular EM field, at microwave frequencies, synchronized with an electron wave packet, intentionally keeps the electron wave packets in a Lagrange type orbit. The Trojan wave packet experiments built on previous work with lithium atoms in an excited state. These are atoms, which respond sensitively to electric and magnetic fields, have decay periods that are relatively prolonged, and electrons, which for all intents and purposes actually operate in classical orbits. The sensitivity to electric and magnetic fields is important because this allows control and response by the polarized microwave field.

Beyond single electron wave packets

In physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere.

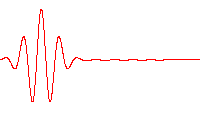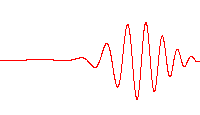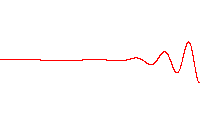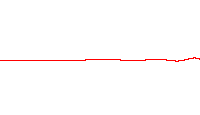
The next logical step is to attempt to move from single electron wave packets to more than one electron wave packet. This had already been accomplished in barium atoms, with two electron wave packets. These two were localized. However, eventually, these created dispersion after colliding near the nucleus. Another technique employed a nondispersive pair of electrons, but one of these had to have a localized orbit close to the nucleus. The nondispersive two-electron Trojan wave packets demonstration changes all that. These are the next step analogue of the one electron Trojan wave packets – and designed for excited helium atoms.

As of July 2005, atoms with coherent, stable two-electron, nondispersing wave packets had been created. These are excited helium-like atoms, or quantum dot helium (in solid-state applications), and are atomic (quantum) analogues to the three body problem of Newton's classical physics, which includes today's astrophysics. In tandem, circularly polarized electromagnetic and magnetic fields stabilize the two electron configuration in the helium atom or the quantum dot helium (with impurity center). The stability is maintained over a broad spectrum, and because of this, the configuration of two electron wave packets is considered to be truly nondispersive. For example, with the quantum dot helium, configured for confining electrons in two spatial dimensions, there now exists a variety of trojan wave packet configurations with two electrons, and as of 2005, only one in three dimensions. In 2012 an essential experimental step was undertaken not only generating but locking the Trojan wavepackets on adiabatically changed frequency and expanding the atoms as once predicted by Kalinski and Eberly. It will allow to create two electron Langmuir Trojan wave packets in Helium by the sequential excitation in adiabatic Stark field able to produce the circular one-electron aureola over He⁺
first and then put the second electron in similar state.

See also

• Atomic orbital
• Rydberg state
• Soliton wave
• Quantum scar
• Gausson

Further reading

Books

• March, Raymond E.; John F. J. Todd (1995). Practical Aspects of Ion Trap Mass Spectrometry: Volume I: Fundamentals of Ion Trap Mass Spectrometry. USA: CRC Press. ISBN 978-0-8493-4452-7.
• March, Raymond E.; John F. Todd (2005). Quadrupole Ion Trap Mass Spectrometry (2 ed.). Wiley, John & Sons, Incorporated. ISBN 978-0-471-48888-0.

Journal articles

• Sirko, L.; Koch, P. M. (1995). "The pendulum approximation for the main quantal resonance in periodically driven Hydrogen atoms". Applied Physics B: Lasers and Optics. 60: S195–S202.
• Klar, H. (1989). "Periodic orbits in atomic hydrogen exposed to circularly polarised laser light". Zeitschrift für Physik D. 11 (1): 45–52. Bibcode:1989ZPhyD..11...45K. doi:10.1007/BF01436583. S2CID 123113349.
• Maeda, H.; Gurian, J. H.; Gallagher, T. F. (2009). "Nondispersing Bohr Wave Packets". Physical Review Letters. 102 (10): 103001–103004. Bibcode:2009PhRvL.102j3001M. doi:10.1103/PhysRevLett.102.103001. PMID 19392109.
• Stroud, C. R. Jr. (2009). "An astronomical solution to an old quantum problem". Physics. 2: 19. Bibcode:2009PhyOJ...2...19S. doi:10.1103/Physics.2.19.

External links

• Aharonov-Bohm Oscillations In "Trojan Electrons"
• Experimental creation of "Trojan Wave Packets" - Barry Dunnings's talk on youtube
• Multi-electron extensions of "Trojan Wave Packets" - Matt Kalinski's talk (1) on youtube
• Multi-electron extensions of "Trojan Wave Packets" - Matt Kalinski's talk (2) on youtube
• Opposite phenomenon - Cycloatoms (PPT Presentation by Robert Wagner)- accelerated counterintuitive relativistic spreading of the sharp Gaussian wave packet originally resembling the ground state into the ring in the hydrogen atom in the ultra-strong magnetic and the laser fields (animation)