User:Brews ohare/Brews ohare/Wavepacket

From Wikipedia, the free encyclopedia

Spatial and temporal relationships[edit]

The mathematical form for the forward propagating wave F involves the argument θ, given by:

Using θ, the amplitude of the forward propagating wave is:

which shows a particular value of u corresponds to a particular value of θ. As time advances, the term (−vt) in θ continuously reduces θ, so the position x corresponding to a chosen value of θ must increase according to:

in order that the value of θ stay the same. In other words, the position x where the amplitude u has the value F(θ) moves in time with the wave speed v. Thus, the particular mathematical form x − vt expresses the traveling nature of the wave. Any function F(x − vt) propagates as a wave of fixed shape moving through space with velocity v.

In the case of a periodic function F with period λ, F(θ + λ) = F(θ), and the periodicity in θ shows that a snapshot of the wave at a given time finds the wave undulating in space, while an observation of the wave at a fixed location finds the wave undulating in time.[1] For example, a repetition in time occurs when θ increases by the period of F; suppose time increases by an amount Δt so that:[2]

Then the periodicity of F shows F is unchanged provided Δt has the particular value Δt = T given by:

The time T is therefore the period of the wave in time and is related to the wavelength and wave speed. Likewise, a repetition in space occurs when x increases an amount Δx enough to cause an increase in θ by λ:

which means F is unchanged provided:

which means the periodicity λ of the function F is also the wavelength of the wave. In summary, the temporal variation in u with period T at a fixed location is related via the wave speed v to the corresponding spatial variation with wavelength λ at a fixed time.

In particular, the sine is a periodic function and that is why a wave based upon the sine has a wavelength and a period.[3] The sinusoidal wave solution might seem to be a specific solution, not applicable to more complicated propagating waves. For instance, the sinusoid is defined for all times and distances, whereas in physical situations we deal with waves that exist for a limited span in space and duration in time. Fortunately, an arbitrary wave shape F(x − vt) can be decomposed into a set of sinusoidal waves using Fourier analysis. As a result, solutions describing the simple case of a single sinusoidal wave can be applied to more general cases.[2]

Wave packets and the de Broglie wavelength[edit]

A traveling wave packet that might represent a moving particle localized in space

Louis de Broglie postulated that all particles with momentum have a wavelength

where h is Planck's constant, and p is the magnitude of the momentum of the particle. This hypothesis was at the basis of quantum mechanics. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electrons in a CRT display have a De Broglie wavelength of about 10–13 m.

A wave representing such a particle traveling in the k-direction is expressed by the wave function:

where the wavelength is determined by the wave vector k as:

and the momentum by:

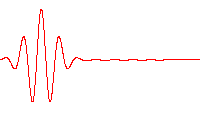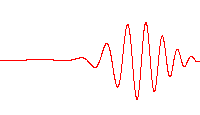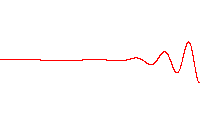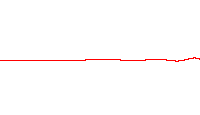
However, a wave like this with definite wavelength is not localized in space, and so cannot represent a particle localized in space. To localize a particle, de Broglie proposed a superposition of different wavelengths ranging around a central value in a wave packet,[4] a waveform often used in quantum mechanics to describe the wave function of a particle. In a wave packet, the wavelength of the particle is not precise, and the local wavelength deviates on either side of the center wavelength value.

In representing the wave function of a particle, the wave packet is often taken to have a Gaussian shape and is called a Gaussian wave packet. [5]Gaussian wave packets also are used to analyze water waves.[6]

For example, a Gaussian wavefunction ψ might take the form:[7]

at some initial time t = 0, where the central wavelength is related to the central wave vector k0 as λ0 = 2π / k0. It is well known from the theory of Fourier analysis,[8] or from the Heisenberg uncertainty principle (in the case of quantum mechanics) that a narrow range of wavelengths is necessary to produce a localized wave packet, and the more localized the envelope, the larger the spread in required wavelengths. The Fourier transform of a Gaussian is itself a Gaussian.[9] Given the Gaussian:

the Fourier transform is:

The Gaussian in space therefore is made up of waves:

that is, a number of waves of wavelengths λ such that kλ = 2 π.

The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined by 1/σ. That is, the smaller the extent in space, the larger the extent in k, and hence in λ = 2π/k.

Wavelength and mathematics of general waveforms[edit]

Wavelength of an irregular periodic waveform at a particular moment in time; the same wavelength marks the distance between similar positions in the waveform.[10]
Various local wavelengths on a crest-to-crest basis in an ocean wave approaching shore.[11]
A propagating wave packet; in general, the envelope of the wave packet moves at a different speed than the constituent waves.[12]

General waveforms, of course, include many different types of wave, and their mathematical description varies, as does the role of wavelength.

A wave of rigid shape traveling in space in the x-direction with wave speed v is described by the functional form:[13]

a form introduced by d'Alembert in connection with the wave equation.[14] There is no role of wavelength for the most general wave of this form, but specialization to a traveling periodic wave does introduce a wavelength though a requirement for periodicity imposed upon the function f:

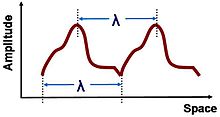
showing that for such a wave the wavelength is the spatial period of the now periodic function f. This wavelength can be measured between any two similarly situated points on the waveform, such as between adjacent maxima (crests) or minima (troughs). See the figure.

Even if f is not a periodic function, wavelength can be a useful concept. For example, in an ocean wave approaching shore, shown in the figure, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.[11]

The notion of a local wavelength also may be applied to a wave packet, which is a superposition of sinusoidal waves with closely spaced wavelengths[15] that result in a waveform that is nearly zero everywhere (due to interference), except in the vicinity of one location.[16][17] Mathematically, a wave packet may be represented as:

where A(k) is the amplitude of the contribution of the wave of wave vector k.[18] The constituent waves have their wavelengths, and the wave packet has an envelope that describes the overall amplitude of the wave. Within the envelope, the distance between adjacent peaks or troughs is a local wavelength,[19] which differs slightly from point to point within the envelope, but is within a range of wavelengths related to those forming the packet.[17][20] In general, the envelope of the wave packet moves at a different speed than the constituent waves.[12] Among other applications, wavepackets are used to model particles in quantum mechanics and to propagate information using lightwaves in fibers.[21]

References[edit]

  1. ^ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN 0470185902. … a periodic wave is any function f(x) whose value varies in a repetitive and perfectly predictable manner over discrete intervals of some variable x.
  2. ^ a b Seth Stein, Michael Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785.
  3. ^ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358.
  4. ^ Ming Chiang Li (1980). "Electron Interference". In L. Marton & Claire Marton (ed.). Advances in Electronics and Electron Physics. Vol. 53. Academic Press. p. 271. ISBN 0120146533.
  5. ^ See for example Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2 ed.). Springer. p. 60. ISBN 3540674586. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. p. 57. ISBN 0521620058.,Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. ISBN 0521658411. {{cite book}}: Text "page 17" ignored (help).
  6. ^ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd ed.). World Scientific. p. 47. ISBN 9971507897.
  7. ^ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2nd ed.). Springer. p. 60. ISBN 3540674586.
  8. ^ Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3rd ed.). Springer. p. 23. ISBN 0387951415.
  9. ^ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. p. 677. ISBN 0521598273.
  10. ^ Cite error: The named reference McPherson was invoked but never defined (see the help page).
  11. ^ a b Paul R Pinet. op. cit. p. 242. ISBN 0763759937.
  12. ^ a b A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN 0486667413. (p. 61) …the individual waves move more slowly than the packet and therefore pass back through the packet as it advances
  13. ^ J Billingham & AC King (2001). Wave Motion. Cambridge University Press. pp. 8 ff. ISBN 0521634504.
  14. ^ For example, the classic d'Alembert solutions to the wave equation take the form of two such waves propagating in opposite directions with the same wave speed: See Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13–14.
  15. ^ William Lowrie (1997). Fundamentals of Geophysics. Cambridge University Press. p. 99. ISBN 0521467284. The packet of energy that propagates as a surface wave contains a spectrum of wavelengths. The energy in the wave propagates as the envelope of the wave packet at a speed that is called the group velocity. The individual waves that make up the wave packet travel with the phase velocity.
  16. ^ See Figure 2.5 in Richard Wallace Robinett (2006). Quantum mechanics (2nd ed.). Oxford University Press. p. 43. ISBN 0198530978.
  17. ^ a b Donald D. Fitts (1999). "§1.2 Wave packet". Principles of quantum mechanics. Cambridge University Press. pp. 8 ff. ISBN 0521658411.
  18. ^ K Griepenkerl, S Bohrmann & Klaus Horn (2006). "§9.3.4 Waves with different frequencies". In Walter Benenson, John W. Harris, Horst Stöcker (ed.). Handbook of Physics (3rd ed.). Springer. p. 300. ISBN 0387952691.{{cite book}}: CS1 maint: multiple names: editors list (link)
  19. ^ Jeffery Cooper (1998). Introduction to partial differential equations with MATLAB. Springer. p. 272. ISBN 0817639675. The local wavelength λ of a dispersing wave is twice the distance between two successive zeros.…the local wave length and the local wave number k are related by k = 2π / λ.
  20. ^ J. David N. Cheeke (2002). "§ 2.2.3 Dispersion, group velocity, and wave packets". Fundamentals and Applications of Ultrasonic Waves. CRC Press. pp. 35 ff. ISBN 0849301300.
  21. ^ Akira Hasegawa, Masayuki Matsumoto (2002). "Information transfer in optical fibers and evolution of the lightwave packet". Optical solitons in fibers (3rd ed.). Springer. pp. 19 ff. ISBN 3540436952.
Retrieved from "https://en.wikipedia.org/w/index.php?title=User:Brews_ohare/Brews_ohare/Wavepacket&oldid=300610768"