User:Brews ohare/Wavelength
More general waveforms[edit]

The figure shows a wave in space in one dimension at a particular time. A wave with a fixed shape but moving in space is called a traveling wave. If the shape repeats itself in space, it is also a periodic wave.[1][2] To an observer at a fixed location, the amplitude of a traveling periodic wave will appear to vary in time, and if its velocity is constant, will repeat itself with a certain period, say T. Assuming one dimension, the wave thus recurs with a frequency, say f, given by:
Every period, one wavelength of the wave passes the observer, showing the velocity of the wave, say v, to be related to the frequency by:
which implies the wavelength is related to frequency as:
Therefore, the results presented above for the sinusoidal wave apply to general waveforms as well.
Formal description[edit]

In one dimension, a traveling wave that propagates without changing shape is described by the equation[3][4]
where f is an arbitrary function of its argument, y = wave amplitude, v = wave speed or velocity, x = position in the wave, and t = time. If we define a particular value of the argument, say xt given by:
then a fixed value of xt is located at a position x that travels in time with a speed v, which means the point in the wave with amplitude y = f (xt) also travels in time with speed v.
To possess a wavelength the waveform must be periodic, which requires f(x) to be a periodic function. That is, f(x) is restricted to functions such that:
which recaptures the relation between wavelength and wave speed found intuitively above: λ = vT.
Connection to sinusoidal waves: components with many wavelengths[edit]

Under rather general conditions, a function f(x) can be expressed as a sum of basis functions {φn(x)} in the form:[6]
known variously as Fourier series, Fourier-Bessel series, generalized Fourier series, and so forth, depending upon the basis used.
For a periodic function f with spatial periodicity λ, the basis functions satisfy φn(x + λ) = φn(x). This condition can be satisfied by basis functions that repeat more often in space than does f itself, and so have wavelengths shorter than the function f.
In particular, for such a periodic function f , the basis may be chosen as a set of sinusoidal functions, selected with wavelengths λ/n (n an integer) to ensure φn(x + λ) = φn(x). For a sine wave sin(kx) the implication is kλ = 2nπ (n an integer), or k = 2πn/λ, where k is called the wave vector and n is called the wavenumber. The wavelength of sin(kx) = sin(2πn x /λ) is λ/n. In this case, the basis function with wavelength λ is referred to as the fundamental and the other basis functions as harmonics. Many examples of such representations are found in books on Fourier series. For example, application to a number of sawtooth waves is presented by Puckette.[7]
Whatever the basis functions, the wave becomes:
Thus, all the components must travel at the same rate to insure that the waveform remains unchanged as it moves. To turn this discussion upside down, because a general waveform may be viewed as a superposition of shorter wavelength basis functions, a requirement upon the physical medium propagating a traveling wave of fixed shape is that the medium must be capable of propagating disturbances of different wavelengths at the same wave speed. This requirement is met in many simple wave propagating mediums, but is not a general property of all media. More commonly, a medium has a non-linear dispersion relation connecting wave vector to frequency of oscillation, and the medium is dispersive, which means propagation of rigid waveforms is not possible in general, but requires very particular circumstances.
Such circumstances sometimes do occur in nonlinear media. For example, in large-amplitude ocean waves, due to properties of the nonlinear surface-wave medium, wave shapes can propagate unchanged.[8] A related phenomenon is the cnoidal wave, a periodic traveling wave named because it is described by the Jacobian elliptic function of m-th order, usually denoted as cn (x; m).[9] Another is the wave motion in an inviscid incompressible fluid, where the wave shape is given by:[10]
one of the early solutions to the Korteweg–de Vries equation of 1895. Here β is a constant related to height of the wave and depth of the water. The Korteweg-de Vries equation is an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. The solutions include examples of solitons, traveling waves without a wavelength because they are not periodically recurring, but still capable of representation as sums of functions with definite wavelengths using the Fourier integral.
Local wavelength[edit]



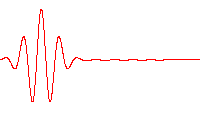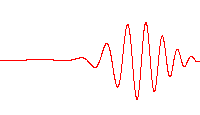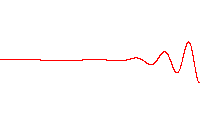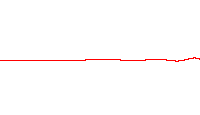
The definition of wavelength as the distance between similar positions in a periodic wave is shown in the two top figures at the right. This wavelength describes the true periodicity of the wave, but in the case of waves that contain a slowly varying amplitude and a much more rapid internal wavelike structure, the local wavelength is a useful idea. The local wavelength is twice the distance between two adjacent internal nodes of the waveform, or the distance between adjacent interior crests or between adjacent interior troughs.[11] In the case of carrier modulation (the carrier is the high frequency internal wave motion), the envelope of the wave form modulating the carrier wave introduces a distribution of local wave lengths in the vicinity of the wavelength of the carrier.[12][13]
A very common example of this situation occurs in the wave packet, a waveform often used in quantum mechanics to describe the wave function of a particle. In the case of a single, isolated wave packet, the only wavelength is the local wavelength, because the envelope does not repeat itself periodically.
In representing the wave function of a particle, the wave packet is often taken to have a Gaussian shape and is called a Gaussian wave packet. [14] Gaussian wave packets also are used to analyze water waves.[15] It is well known from the theory of Fourier analysis,[16] or from the Heisenberg uncertainty principle (in the case of quantum mechanics) that a narrow range of wavelengths is necessary to produce a localized wave packet, and the more localized the envelope, the larger the spread in required wavelengths. The Fourier transform of a Gaussian is itself a Gaussian.[17] Given the Gaussian:
the Fourier transform is:
The Gaussian in space therefore is made up of waves:
that is, a number of waves of wavelengths λ such that kλ = 2 π.
The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined by 1/σ. That is, the smaller the extent in space, the larger the extent in k, and hence in λ = 2π/k.
References[edit]
- ^ a b Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN 0470185902.
- ^ Robert Prigo (2007). Making physics fun. Corwin Press. pp. 80 ff. ISBN 1412926637.
- ^ J Billingham & AC King (2001). Wave Motion. Cambridge University Press. pp. 8 ff. ISBN 0521634504.
- ^ For example, the classic d'Alembert solutions to the wave equation take the form of two such waves propagating in opposite directions with the same wave speed: See Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13–14.
- ^ Stanley J Farlow (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publications. p. 82. ISBN 048667620X.
- ^ See for example, Gerald B Folland (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. pp. 77 ff. ISBN 0821847902.
- ^ Miller Puckette (2007). The theory and technique of electronic music. World Scientific. ISBN 9812700773.
- ^ Ken'ichi Okamoto (2001). Global environment remote sensing. IOS Press. p. 263. ISBN 9781586031015.
- ^ Roger Grimshaw (2007). "Solitary waves propagating over variable topography". In Anjan Kundu (ed.). Tsunami and Nonlinear Waves. Springer. pp. 52 ff. ISBN 3540712550.
- ^ P. G. Drazin, R. S. Johnson (1996). Solitons: an introduction. Cambridge University Press. p. 8. ISBN 0521336554.
- ^ Jeffery Cooper (1998). Introduction to partial differential equations with MATLAB. Springer. p. 272. ISBN 0817639675.
- ^ John J O'Reilly (1989). Telecommunications Principles (2 ed.). Springer. pp. 58 ff.
- ^
Martin Russ (1996). Sound synthesis and sampling. Focal Press. p. 117. ISBN 0240514297.
For a sine carrier and non-sinusoidal wave modulator, there are actually the equivalent of several modulator frequencies: one for each harmonic in the modulator.
- ^
See for example Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2 ed.). Springer. p. 60. ISBN 3540674586. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. p. 57. ISBN 0521620058. and Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. ISBN 0521658411.
{{cite book}}: Text "page 17" ignored (help) - ^ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd ed.). World Scientific. p. 47. ISBN 9971507897.
- ^ Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3rd ed.). Springer. p. 23. ISBN 0387951415.
- ^ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. p. 677. ISBN 0521598273.
Further reading[edit]
- Kenneth Davíes (1990). Ionospheric radio. IEE. pp. 9 ff. ISBN 086341186X. Discussion of modulated wave propagation
- google book search









![{\displaystyle y=A\ \mathrm {sech} ^{2}[\beta (x-vt)]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad8289edf0d38cfbbcfb0676eb1d02ab8d9bc785)



