User:Merdrach/sandbox

Part of the DISC1 interactome with genes represented by text in boxes and interactions noted by lines between the genes. From Hennah and Porteous, 2009.

Complex dynamics of molecular networks

In molecular biology, a molecular network is a set of molecular interactions in a particular cell. The term specifically refers to physical interactions among molecules but can also mean indirect interactions among genes, i.e. genetic interactions. The alternative word "interactome" was originally coined in 1999 by a group of French scientists headed by Bernard Jacq.

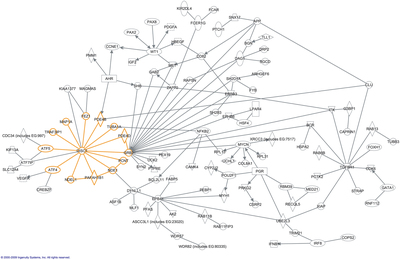
In depth molecular analysis of living organisms has highlighted the fact that biological functions can rarely be attributed to the individual action of cellular components, but often relies on complex interactions between the cell’s numerous components such as proteins, RNA, DNA and other small molecules . These interactions can be intracellular, intercellular or even across tissues. The complexity of biological networks lies in the fact that there are large numbers of functionally diverse interacting entities which are frequently multifunctional. To further increase the complexity entities act in a selective and non linear fashion . The underlying principles that govern these networks are beginning to be elucidated, and it has become apparent these principles share many characteristics with other forms of complex networks such as the internet, computer chips and society . The detailing of large, well-mapped, non-biological systems can be gleaned and transposed to some degree, to characterize the intricate interwoven relationship that mediate cellular function. A molecular network does not exist as a static entity, thus to fully appreciate the functionality of the system it needs to be viewed dynamically – over time. Therefore, dynamical modeling of molecular networks gives a complete representation of a network’s complexity.

Molecular Networks

The applications of technologies such as microarrays has provided a clearer picture of the multitude of simultaneous process taken place in a cell at a given point. Whilst even more cutting edge technologies such as yeast two hybrid screens and protein chips have helped to understand how and when different molecules are interacting . Each interaction taking place can be fit into various networks such as genetic, signaling, regulatory, metabolic and protein networks. It is rare that a molecular network will act in isolation but rather many of the examples in the categories above will overlap with one another forming a network of networks.

To reconstruct a quantifiable network we need to incorporate several definable factors:

• The nodes, also referred as vertices or network elements, are the reacting substrate. In molecular systems these can be DNA, RNA, proteins or other macromolecules.
• Connections, also referred to as interactions, links or transitions, can be defined as the physical or functional interaction of the nodes .

The combinations of these form the network, more formally known as a graph.

File:Net image a C2Nn4hsmFgTF high res.png

Fig. 1 - Example of a network (Source: String)

The degree (K) refers to the amount of connections that each node (N) contains. These can be reversible or irreversible, in the later the can be defined in terms of “in” and “out”. A network may possess a clear directed orientation, for example in a metabolic network, where the nodes are metabolites and the connections are enzyme catalysed reactions, many of the reactions are irreversible and therefore form a directed network. The degrees, termed “in” or “out” determine the number of reactions that produce or consume it. . Contrary, a non – directed network containing many reversible reactions could involve protein-protein interactions in which the binding of protein A to B also involves the binding of protein B to A (Fig.2).

Fig. 2 - Example of undirected and directed network

The average degree (P) is the averaged number of (K) across all nodes. The degree distribution [P(k)] is the probability of a randomly selected node having a degree of (K) . A plot of [P(k)] versus (K) allows for the characterisation of the type of network. A random network, follows the Poisson style distribution showing most nodes have approximately the name number of connections. However, studies into complex biological networks including protein – protein networks, genetic regulatory networks and metabolic networks have shown that they tend not to possess a Poisson distribution. Instead they exhibit a power law distribution in which it is far more unlikely for a node to contain (k) connections, most nodes will have low degrees but those few with high degrees are referred to as hubs. This type of network is referred to as a scale free network, and in these a relatively few hubs will often determine main characteristics of the network(Fig.3).

Fig. 3 - Example of Poisson distribution graph and Power law distribution graph

A study involving the metabolic networks of 43 organisms, representing each different kingdom of life, showed that when each node was ranked by degree (k) many nodes had few connections, whilst a few nodes had many connections, typical of a scale free network. What’s more is that these hubs were remarkably similar across each different kingdom, with substrates such as ADP, orthophosphate, L-glutamate and pyrophosphate having high a (K) in each organism. These highly connected substrates may determine many of the characteristics of metabolic networks. Random and scale-free networks both possess what is known as a small world effect. This refers to the fact that the number of connections that need to be crossed between any two nodes is relatively small. In scale-free networks this distance is even smaller and can be referred to as ultra-small world. The advantage of the small world effect from a cellular perspective is the ability to efficiently respond to either internal errors or environmental changes. For example if an organism was suddenly faced with exhaustion of a substrate required for growth then a small world network would allow for a perturbation to be registered across the whole network very quickly. Also, a change in catabolic pathways may necessitate activation of longer biochemical process in the catabolism of an alternative. A small world effect means that the distance of the alternative network pathway is shortened, requiring less resources enzyme synthesis.

Dynamic Modelling

To fully understand complexity of a network, application of differential equations is essential to demonstrate and quantify dynamics. To illustrate this, a simplified model based on a signaling network but containing only a few nodes, complete with dynamics, has been provided (see below). This is an example of classical dynamic study which depends on the change of molecules concentration over time. In silico perturbations can also be carried out to examine the effect of any specific modification on the network as a whole. Modeling dynamics within a eukaryotic cells introduces an extra level of complexity due to their subcellular compartmentalization. Compartments like the nucleus, mitochondria, Golgi apparatus and many others, each have different environmental factors ie different pH, ion concentration and overall molecular composition. In other words, a protein exhibiting a specific tertiary structure in a compartment may not exhibit the same structure in another, which can affects the overall reactivity of this protein especially if it were an enzyme. Modifications caused by environmental factors can have an effect on the entire downstream molecular pathway. In our simplified model below, A represents an upstream node and E represents a downstream nodes whereas B, C and D are intermediates.

In order to comprehend the dynamics of the network, the following terms need to be clarified:

• Deterministic or stochastic: The former is used when all the reactive species are known, such as in a defined chemical system, but the latter is commonly used in a complex system such as the living cell all reacting species are not fully known.
• Continuous or discrete time: The former is commonly used to describe most signaling pathways models using ordinary differential equations (ODE), and the latter is used in cases such as a protein in one cell interacting with a protein found in another cell.
• Continuous or discrete state: The former is normally used because of the regular pattern reactions follow. The latter, however, can be used to describe a gene that is expressed under special conditions (repressor removal).
• Partially differential equations: Similar to ODE but allows division of the system into discrete parts, rather than one continuous and homogeneous model, to give a more realistic image of the dynamics of each step of the molecular network.
• Hybrid models: These exist to describe pathways that illustrate both continuous dynamics and discrete states.

To explain ordinary differential equations (ODE), a biochemical reaction is introduced as a simple model, or a section of an entire metabolic pathway. Assuming the five biomolecules (A, B, C, D and E) components of a biological system, using the low of mass action, overall reaction can be represented as follows:

The law of mass action depends on the concentration of each substrate, and consequently on the collision probability among the substrates allowing the chemical reaction to happen and the product to be produced. Firstly, the system contained only A and B. If these two substrates are found in an appropriate initial concentration, reaction 1 takes place producing C with a reaction constant k1. C is dissociating back into A and B with a reaction constant k2 and also into A and D with a reaction constant k3. D is converted to E in another reaction with the constant k4.

Studying these reactions in terms of concentration change over time is considered to be a dynamical study, which in this case is simple rather than complex. The reduction of concentration of substrates A or B over time equals the increase of the concentration of product C, and this can be expressed using the law of mass action as follows:

$-{\frac {d[A]}{dt}}=-{\frac {d[B]}{dt}}={\frac {d[C]}{dt}}$

And similarly:

$-{\frac {d[C]}{dt}}={\frac {d[A]}{dt}}={\frac {d[D]}{dt}}$

$-2{\frac {d[D]}{dt}}={\frac {d[E]}{dt}}$

Another way to express the reaction velocity can be given in terms of the reaction constants k; where the reaction velocity equals the multiplication of the reaction constant by the concentrations of the substrates at a specific moment:

$(1){\begin{cases}v_{1}=k_{1}[A][B]\,\operatorname {expresses\,the\,reaction} \,A+B{\xrightarrow[{}]{k_{1}}}C\\v_{2}=k_{2}[C]\,\operatorname {expresses\,the\,reaction} \,C{\xrightarrow[{}]{k_{2}}}A+B\\v_{3}=k_{3}[C]\,\operatorname {expresses\,the\,reaction} \,C{\xrightarrow[{}]{k_{3}}}A+D\\v_{4}=k_{4}[D]^{2}\,\operatorname {expresses\,the\,reaction} \,2D{\xrightarrow[{}]{k_{4}}}E\end{cases}}$

Above, reactant C is an intermediate product for reaction 1 and substrate for reaction 2 and 3, and there are many intermediate compounds in molecular pathways whose concentration does not show a significant change (increase or decrease) since it is being constantly reacting. Since the anabolism rate of compound C is equal to its catabolism rate, this can be expressed as follows:

Here, [C] is a constant under quasi steady state condition

${\frac {d[C]}{dt}}0$

$k_{1}[A][B]=k_{2}[C]+k_{3}[C](2)$

Anabolism rate = catabolism rate

Reaction 1 rate = Reaction 2 and Reaction 3 rates

Anabolism rate = Catabolism rate Reaction 1 rate = Reaction 2 and reaction 3 rates

As the concentration of A increases, both the concentrations of B and C decrease in order to maintain the equilibrium state. The opposite is also correct. But if the concentration if B is assumed to be constant, then the relation between A and C can be expressed as follows:

$[A]+[C]=A_{0}(3)$ (A₀ is constant)

From equations 1 and 2 and in terms of B and C:

$[C]={\frac {A_{0}[B]}{K_{m}}}+[B](4)$

Where Km = k2 + k3 / k1 is called the Michaelis-Menten constant.

The concentration of each of the molecules can be expressed in terms of the velocity of each reaction:

$(5){\begin{cases}{\frac {d[A]}{dt}}=-v_{1}+v_{2}+v_{3}\\{\frac {d[B]}{dt}}=-v_{1}+v_{2}\\{\frac {d[C]}{dt}}=v_{1}-v_{2}-v_{3}\\{\frac {d[D]}{dt}}=v_{3}-2v_{4}\\{\frac {d[E]}{dt}}=v_{4}\end{cases}}$

The positive sign refers to molecule anabolism, and the negative to catabolism. Substituting equations 1 and 4 in 5 results:

$(6){\begin{cases}{\frac {d[A]}{dt}}=0\\{\frac {d[B]}{dt}}={\frac {-k_{3}A_{0}[B]}{K_{m}+[B]}}\\{\frac {d[C]}{dt}}=0\\{\frac {d[D]}{dt}}={\frac {k_{3}A_{0}[B]}{K_{m}+[B]}}-2k_{4}[D]^{2}\\{\frac {d[E]}{dt}}=k_{4}[D]^{2}\end{cases}}$

Equation 6 can be reduced into:

$(7){\begin{cases}{\frac {d[B]}{dt}}={\frac {-k_{3}A_{0}[B]}{K_{m}+[B]}}\\{\frac {d[D]}{dt}}={\frac {k_{3}A_{0}[B]}{K_{m}+[B]}}-2k_{4}[D]^{2}\\{\frac {d[E]}{dt}}=k_{4}[D]^{2}\end{cases}}$

Equation 7 expresses the overall dynamics of each molecule in the network. This study is based on molecules concentration, but does this simple study reflect really the complex dynamics of molecular network? Since there is no explicit definition of complexity, an analogy of chemical reactions can be introduced. An example of a single reaction study is the Brownian ratchet study of actin filament polymerisation, and another about a multiple reaction study is the study of the pathway of cellular signaling. The analogy mentioned above may give an idea of how complexity can be described in terms of the quantity and the quality of the reacting species within a molecular network (Rangamani & Iyengar, 2008). In addition, the above is an example of a simple linear study that examines the interactivity of only five species (nodes) using ODE. However, in practice modeling dynamics of molecular networks may investigate much larger numbers of species, and may also require the additional use of PDE to examine dynamics. Due to the fact that these molecular interactions are concentration dependent, the following dynamical study shows how these concentrations are estimated in terms of production and loss rates for each protein.

The rate of change of a protein (P) concentration in a living cell is a function of the production rate (α) of that protein and the removal rate (β) of that protein. Mathematically, this can expressed as follows:

${\frac {d[P]}{dt}}$$=\alpha -\beta [P](8)$

The production rate is a multi-step process that includes: the rate of transcription factor binding to the promoter site, mRNA synthesis, protein synthesis and finally a protein that has action in the cytosol. The first three steps are neglected because of the short time required and to simplify the study.

The removal rate (β) is directly correlated with the concentration of P. In fact β is a function of P, where it increases when P increases, and vice versa. β can be mathematically expressed as follows:

$\beta =\beta 1+\beta 2$

Where β1 is the degradation rate, which describes how stable is the protein synthesized, β2 is the dilution rate, which describes how the protein concentration is halved every time the cell divides.

Case 1: Steady state (s. s.)

${\frac {d[P]}{dt}}=0$; because the rate of change is constant, and the derivative of any constant is zero. From equation 8:

${\frac {d[A]}{dt}}$$=\alpha -\beta [P]=0$

$\alpha -\beta [P]=0$

$\alpha =\beta [P]$

$[P]={\frac {\alpha }{\beta }}$ (Steady state condition 9)

Equation 9 means that the concentration of a protein P in the cell at a steady state condition equals to the production rate over the removal rate.

Case 2: Protein suppression

Starting from the steady state condition, and from equation 8 where α = 0

${\frac {d[P]}{dt}}=-\beta [P]$

Integrating both sides:

$P=P_{ss}e^{-\beta t}(10)$

Equation 11 can be illustrated similarly to a radioactive compound decay curve:

Case 3: Protein production is switched on:

Starting from the steady state condition, by integrating equation 8:

${\frac {d[P]}{dt}}$ = New state – loss

On integration:

$P(t)=P_{ss}-P_{ss}e^{-\beta t}$

$P(t)=({\frac {\alpha }{\beta }})(1-e^{-\beta t})(11)$

The study above describes the dynamics of one protein within a molecular network. As a molecular network contains numerous proteins, and other sorts of molecules, each involved species should be studied extensively to give a reliable model of the dynamical behavior of a molecular network.

Stochasticity

The problem with biological systems is the randomness and the non-deterministic behavior, in comparison with well-defined chemical systems. This is because the relatively higher number and the huge variety of the involved species within a biological system than those in a chemical system. For a living cell, of about 1µm x 1µm x 0.1µm = 0.1 µm3 in volume, the environment is not in fact entirely heterogeneous, especially in eukaryotic cells that include many subcellular compartments (Golgi apparatus, mitochondria etc.). Thus, another layer of complexity is added due to the different rates of diffusivity for each molecule within a network. In each part of the cell, and for each molecule, diffusivity is determined by the diffusion coefficient (DC) which has a physical dimension of surface per time [L]2 / [T]. DC describes how fast a molecule is transported within a fluid depending on the physical properties of the molecule. As a result, the dynamics of a molecular network can be studied when the movement of each species of the network is defined. For example, DC of cAMP, the ubiquitous second messenger, is 300 µm2/s in the cytoplasm and the DC of phosphatidylinositol 4,5-bisphosphate in the membrane is 1 µm2/s..

To be able to determine the diffusion coefficient, some information needs to be known about each studied molecule such as: polarity, molecular weight and 3D structure. This allows for predictions to be made regarding its movement within the fluid (cytoplasm). In addition, some molecules have many functions in the cell, and can be involved in many molecular networks, which adds another layer of complexity of the dynamics of molecular networks.

Applications in molecular networks

The use of increasing quantities of available data allows for the construction and improvement of dynamic network models. These models can then be used to filter data into useful information concerning: Stimulus -response interactions, Predictions of new molecular targets based on pathway context, Potential use of combinatorial therapies, Pathway responses to stimuli with respect to reactive or compensatory behavior as well as stress and toxic response mechanisms. In silico studies will provide results which can then be used to construct lab experiments in order to validate the development of complex molecular therapeutics. This would be far faster than carrying out all the experimentation in a 'wet-lab' setting, as the number of experiments required to explore the interactions of many genes would be immense.

Predictions of cellular responses to drugs can be made using gene expression data according to higher-order and non-linear correlations. Examples exist of computationally-discovered associations that predicted the drug response from gene expression. Because the relationships are often complex and nonlinear, the ability to input data into a proven model allows for much faster construction of hypotheses that can then be tested for validity. This can even be extended to individual patients - assaying a tumor biopsy for gene expression patterns could provide information enabling the selection of the most appropriate drug for that patient's treatment. Moreover, predictions of proteins functions within the context of networks is possible from high-throughput experiments that are increasingly available from large-scale protein-protein interaction networks. The methods of prediction can be categorised into methods utilising direct connections, and approaches based on extracted clusters. This is achieved by using a functional similarity score that weights proteins by their distance to the target protein, and scores each function based on the frequency of that weight in its neighboring proteins.

Disease prediction is also possible and is achieved through identification of either a phenotypic marker from a monogenic disease as a causal agent, or a gene responsible for the disease development. This is where one input variable predicts one output variable in a simple relationship. However, most prevalent diseases are caused by a complex combinations of factors, which require accurate analysis of the sets of variables that are both directly responsible and indirectly associated. Because these variables can be difficult to identify and group correctly, each variable must be monitored from the start. Experimental data has shown that the separation of related and unrelated factors becomes more accurate as higher-order SNP motifs are examined. Additionally, Phenotypic Disease Networks (PDN) have been proposed with disease phenotypes as nodes. The purpose of these network models is to help establish origins of diseases and predict outcomes of pathogenesis. Furthermore, construction and understanding of signaling networks play a principal role in cancer pathogenesis, migration and metastasis. Specifically, crosstalk between Akt/mTOR pathways and ERK gives an overview of proto – oncogene mutation or tumor suppressor genes and mRNA expression that has a role in disease. Therefore, identifying tumor networks will help to understand tumor resistance in vitro and in vivo.

References

Alon, U. (2006). An Introduction to Systems Biology: Design Principles of Biological Circuits (Mathematical & Computational Biology) (p. 320). Chapman and Hall/CRC.

Barabási, A.-L., & Oltvai, Z. N. (2004). Network biology: understanding the cell’s functional organization. Nature reviews. Genetics, 5(2), 101–13. doi:10.1038/nrg1272

Csermely, P., Korcmaros, T., Kiss, H., & London, G. (2013). Structure and dynamics of molecular networks: A novel paradigm of drug discovery A comprehensive review. Pharmacology & Therapeutics, 76.

Dana Pe’er and Nir Hacohen. (2011). Principles and Strategies for Developing Network Models in Cancer, 144(6), 864–873. doi:10.1016/j.cell.2011.03.001.Principles

Hidalgo, C. a, Blumm, N., Barabási, A.-L., & Christakis, N. a. (2009). A dynamic network approach for the study of human phenotypes. PLoS computational biology, 5(4), e1000353. doi:10.1371/journal.pcbi.1000353

Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., & Barabási, A. L. (2000). The large-scale organization of metabolic networks. Nature, 407(6804), 651–4. doi:10.1038/35036627

Kitano, H. (2002). Computational systems biology. Nature, 420(6912), 206–10. doi:10.1038/nature01254

McLaughlin, S., & Wang, J. (2002). PIP2 and proteins: Interaction, organisation, and information flow. Annual review biophysical biomoleules, 31, 151–75.

Rangamani, P., & Iyengar, R. (2008). Modelling cellular signalling systems. Essays in biochemistry, 45, 83–94. doi:10.1042/BSE0450083

Category:Bioinformatics Category:Molecular biology Category:Systems biology