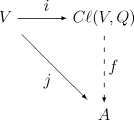User:Prof McCarthy/cliffordalgebra
In mathematics, Clifford algebras are a type of associative algebra. They can be thought of as one of the possible generalizations of the complex numbers and quaternions. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry and theoretical physics. They are named after the English geometer William Kingdon Clifford.
Introduction and basic properties[edit]
Specifically, a Clifford algebra is a unital associative algebra which contains and is generated by a vector space V equipped with a quadratic form Q. The Clifford algebra Cℓ(V,Q) is the "freest" algebra generated by V subject to the condition[1]
If the characteristic of the ground field K is not 2, then one can rewrite this fundamental identity in the form
where <u, v> = ½(Q(u + v) − Q(u) − Q(v)) is the symmetric bilinear form associated to Q, via the polarization identity. The idea of being the "freest" or "most general" algebra subject to this identity can be formally expressed through the notion of a universal property, as done below.
Quadratic forms and Clifford algebras in characteristic 2 form an exceptional case. In particular, if char K = 2 it is not true that a quadratic form determines a symmetric bilinear form, or that every quadratic form admits an orthogonal basis. Many of the statements in this article include the condition that the characteristic is not 2, and are false if this condition is removed.
As a quantization of the exterior algebra[edit]
Clifford algebras are closely related to exterior algebras. In fact, if Q = 0 then the Clifford algebra Cℓ(V,Q) is just the exterior algebra Λ(V). For nonzero Q there exists a canonical linear isomorphism between Λ(V) and Cℓ(V,Q) whenever the ground field K does not have characteristic two. That is, they are naturally isomorphic as vector spaces, but with different multiplications (in the case of characteristic two, they are still isomorphic as vector spaces, just not naturally). Clifford multiplication is strictly richer than the exterior product since it makes use of the extra information provided by Q.
More precisely, Clifford algebras may be thought of as quantizations (cf. quantization (physics), Quantum group) of the exterior algebra, in the same way that the Weyl algebra is a quantization of the symmetric algebra.
Weyl algebras and Clifford algebras admit a further structure of a *-algebra, and can be unified as even and odd terms of a superalgebra, as discussed in CCR and CAR algebras.
Universal property and construction[edit]
Let V be a vector space over a field K, and let Q : V → K be a quadratic form on V. In most cases of interest the field K is either R, C or a finite field.
A Clifford algebra Cℓ(V,Q) is a unital associative algebra over K together with a linear map i : V → Cℓ(V,Q) satisfying i(v)2 = Q(v)1 for all v ∈ V, defined by the following universal property: Given any associative algebra A over K and any linear map j : V → A such that
- j(v)2 = Q(v)1 for all v ∈ V
(where 1 denotes the multiplicative identity of A), there is a unique algebra homomorphism f : Cℓ(V,Q) → A such that the following diagram commutes (i.e. such that f o i = j):
Working with a symmetric bilinear form <·,·> instead of Q (in characteristic not 2), the requirement on j is
- j(v)j(w) + j(w)j(v) = 2<v, w> for all v, w ∈ V.
A Clifford algebra as described above always exists and can be constructed as follows: start with the most general algebra that contains V, namely the tensor algebra T(V), and then enforce the fundamental identity by taking a suitable quotient. In our case we want to take the two-sided ideal IQ in T(V) generated by all elements of the form
- for all
and define Cℓ(V,Q) as the quotient
- Cℓ(V,Q) = T(V)/IQ.
It is then straightforward to show that Cℓ(V,Q) contains V and satisfies the above universal property, so that Cℓ is unique up to a unique isomorphism; thus one speaks of "the" Clifford algebra Cℓ(V, Q). It also follows from this construction that i is injective. One usually drops the i and considers V as a linear subspace of Cℓ(V,Q).
The universal characterization of the Clifford algebra shows that the construction of Cℓ(V,Q) is functorial in nature. Namely, Cℓ can be considered as a functor from the category of vector spaces with quadratic forms (whose morphisms are linear maps preserving the quadratic form) to the category of associative algebras. The universal property guarantees that linear maps between vector spaces (preserving the quadratic form) extend uniquely to algebra homomorphisms between the associated Clifford algebras.
Basis and dimension[edit]
If the dimension of V is n and {e1,…,en} is a basis of V, then the set
is a basis for Cℓ(V,Q). The empty product (k = 0) is defined as the multiplicative identity element. For each value of k there are n choose k basis elements, so the total dimension of the Clifford algebra is
Since V comes equipped with a quadratic form, there is a set of privileged bases for V: the orthogonal ones. An orthogonal basis is one such that
where <·,·> is the symmetric bilinear form associated to Q. The fundamental Clifford identity implies that for an orthogonal basis
This makes manipulation of orthogonal basis vectors quite simple. Given a product of distinct orthogonal basis vectors, one can put them into standard order by including an overall sign corresponding to the number of flips needed to correctly order them (i.e. the signature of the ordering permutation).
If the characteristic is not 2 then an orthogonal basis for V exists, and one can easily extend the quadratic form on V to a quadratic form on all of Cℓ(V,Q) by requiring that distinct elements are orthogonal to one another whenever the {ei}'s are orthogonal. Additionally, one sets
- .
The quadratic form on a scalar is just Q(λ) = λ2. Thus, orthogonal bases for V extend to orthogonal bases for Cℓ(V,Q). The quadratic form defined in this way is actually independent of the orthogonal basis chosen (a basis-independent formulation will be given later).
Examples: real and complex Clifford algebras[edit]
The most important Clifford algebras are those over real and complex vector spaces equipped with nondegenerate quadratic forms. The geometric interpretation of nondegenerate Clifford algebras is known as geometric algebra.
Every nondegenerate quadratic form on a finite-dimensional real vector space is equivalent to the standard diagonal form:
where n = p + q is the dimension of the vector space. The pair of integers (p, q) is called the signature of the quadratic form. The real vector space with this quadratic form is often denoted Rp,q. The Clifford algebra on Rp,q is denoted Cℓp,q(R). The symbol Cℓn(R) means either Cℓn,0(R) or Cℓ0,n(R) depending on whether the author prefers positive definite or negative definite spaces.
A standard orthonormal basis {ei} for Rp,q consists of n = p + q mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1. The algebra Cℓp,q(R) will therefore have p vectors which square to +1 and q vectors which square to −1.
Note that Cℓ0,0(R) is naturally isomorphic to R since there are no nonzero vectors. Cℓ0,1(R) is a two-dimensional algebra generated by a single vector e1 which squares to −1, and therefore is isomorphic to C, the field of complex numbers. The algebra Cℓ0,2(R) is a four-dimensional algebra spanned by {1, e1, e2, e1e2}. The latter three elements square to −1 and all anticommute, and so the algebra is isomorphic to the quaternions H. The next algebra in the sequence is Cℓ0,3(R) is an 8-dimensional algebra isomorphic to the direct sum H ⊕ H called split-biquaternions.
One can also study Clifford algebras on complex vector spaces. Every nondegenerate quadratic form on a complex vector space is equivalent to the standard diagonal form
where n = dim V, so there is essentially only one Clifford algebra in each dimension. We will denote the Clifford algebra on Cn with the standard quadratic form by Cℓn(C). One can show that the algebra Cℓn(C) may be obtained as the complexification of the algebra Cℓp,q(R) where n = p + q:
Here Q is the real quadratic form of signature (p,q). Note that the complexification does not depend on the signature. The first few cases are not hard to compute. One finds that
- Cℓ0(C) = C
- Cℓ1(C) = C ⊕ C
- Cℓ2(C) = M2(C)
where M2(C) denotes the algebra of 2×2 matrices over C.
It turns out that every one of the algebras Cℓp,q(R) and Cℓn(C) is isomorphic to a matrix algebra over R, C, or H or to a direct sum of two such algebras. For a complete classification of these algebras see classification of Clifford algebras.
Example: quaternions[edit]
Quaternions[edit]
Let the vector space V be real three dimensional space R3, and the quadratic form Q be derived from the usual Euclidean metric. Then, for v, w in R3 we have the quadratic form, or dot product,
Now introduce the Clifford product of vectors v and w given by
This formulation uses the negative sign so the correspondence with quaternions is easily shown.
Denote a set of orthogonal unit vectors of R3 as e1, e2, and e3, then the Clifford product yields the relations
and
The general element of the Clifford algebra Cℓ3(R) is given by
The linear combination of the even rank elements of Cℓ(R3) defines the even sub algebra Cℓ+3(R) with the general element
The basis elements can be identified with the quaternion units i, j, k as
which shows that even sub algebra Cℓ+(R3) is Hamilton's real quaternion algebra.
To see this, compute
and
Finally,
Dual quaternions[edit]
Let the vector space V be real four dimensional space R4, and let the quadratic form Q be a degenerate form derived from the Euclidean metric on R3. For v, w in R4 introduce the degenerate quadratic form
This degenerate scalar product projects distance measurements in R4 onto the R3 hyperplane.
The Clifford product of vectors v and w is given by
Note the negative sign is introduced to simplify the correspondence with quaternions.
Denote a set of orthogonal unit vectors of R4 as e1, e2, e3 and e4, then the Clifford product yields the relations
and
The general element of the Clifford algebra Cℓ(R4, d) has 16 components. The linear combination of the even ranked elements defines the even sub algebra Cℓ+3(R4, d) with the general element
The basis elements can be identified with the quaternion units i, j, k and the dual unit ε as
To see this, compute
and
The exchanges of e1 and e4 alternate signs an even number of times, and the result is that ε commutes with the quaternion units i, j, and k.
References[edit]
- ^ Mathematicians who work with real Clifford algebras and prefer positive definite quadratic forms (especially those working in index theory) sometimes use a different choice of sign in the fundamental Clifford identity. That is, they take v2 = −Q(v). One must replace Q with −Q in going from one convention to the other.