User:Tomruen/List of isotoxal polychora and honeycombs
Appearance
A vertex transitive polytope is also edge-transitive if its vertex figure is vertex transitive! (Since each vertex in the vertex figure represents an edges in the polytope)
I think this is a complete list of regular convex and uniform 4-polytopes/honeycombs that are isotoxal. (And a subset of nonconvex forms from the nonconvex regulars)
Linear graph polychora/honeycombs
[edit]From convex self-dual regular and uniform polychora:
| [p,q,p] | {p,q,p} {q,p} |
r{p,q,p} {}x{p} |
2t{p,q,p} s{2,4} |
e{p,q,p} s{2,2q} |
|---|---|---|---|---|
| [3,3,3] | {3,3,3} 
|
r{3,3,3} 
|
2t{3,3,3} 
|
e{3,3,3} 
|
| [3,4,3] | {3,4,3} 
|
r{3,4,3} 
|
2t{3,4,3} 
|
e{3,4,3} 
|
| [5/2,5,5/2] | {5/2,5,5/2} |
r{5/2,5,5/2} |
2t{5/2,5,5/2} DEGENERATE |
e{5/2,5,5/2} DEGENERATE |
| [5/2,5,5/2] | {5/2,5,5/2} |
r{5/2,5,5/2} |
2t{5/2,5,5/2} DEGENERATE |
e{5/2,5,5/2} DEGENERATE |
| [4,3,4] | {4,3,4} 
|
r{4,3,4} 
|
2t{4,3,4} 
|
e{4,3,4} 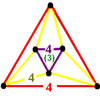
|
| [3,5,3] | {3,5,3} 
|
r{3,5,3} 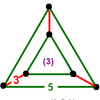
|
2t{3,5,3} 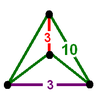
|
e{3,5,3} 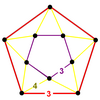
|
| [3,6,3] | {3,6,3} |
r{3,6,3} |
2t{3,6,3} |
e{3,6,3}
|
| [5,3,5] | {5,3,5} 
|
r{5,3,5} 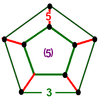
|
2t{5,3,5} 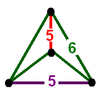
|
e{5,3,5} 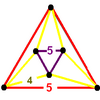
|
| [6,3,6] | {6,3,6} |
r{6,3,6} |
2t{6,3,6} |
e{6,3,6} |
From convex regular and uniform polychora:
| [p,q,r] | {p,q,r} {q,r} |
r{p,q,r} {}x{r} |
r{r,q,p} {p}x{} |
{r,q,p} {q,p} |
|---|---|---|---|---|
| [4,3,3] | {4,3,3} 
|
r{4,3,3} 
|
r{3,3,4} (24-cell) 
|
{3,3,4} 
|
| [5,3,3] | {5,3,3} 
|
r{5,3,3} 
|
r{3,3,5} 
|
{3,3,5} 
|
| [6,3,3] | {6,3,3} |
r{6,3,3} |
r{3,3,6} |
{3,3,6} |
| [5/2,5,3] | {5/2,5,3} |
r{5/2,5,3} |
r{3,5,5/2} |
{3,5,5/2} |
| [5,3,5/2] | {5,3,5/2} |
r{5,3,5/2} |
r{5/2,3,5} |
{5/2,3,5} |
| [3,5/2,5] | {3,5/2,5} |
r{3,5/2,5} |
r{5,5/2,3} |
{5,5/2,3} |
| [3,3,5/2] | {3,3,5/2} |
r{3,3,5/2} |
r{5/2,3,3} |
{5/2,3,3} |
| [5,3,4] | {5,3,4} 
|
r{5,3,4} 
|
r{4,3,5} 
|
{4,3,5} 
|
| [6,3,4] | {6,3,4} |
r{6,3,4} |
r{4,3,6} |
{4,3,6} |
| [6,3,5] | {6,3,5} |
r{6,3,5} |
r{5,3,6} |
{5,3,6} |
Bifurcated graph honeycombs
[edit]| Family | = |
= |
= |
= |
|---|---|---|---|---|
| [3,31,1] |  |
 |
 |
 |
| [4,31,1] |  |
 |
 |
 |
| [5,31,1] |  |
 |
 |
 |
| [6,31,1] |
| Family | = |
= |
= |
= |
|---|---|---|---|---|
| [3,41,1] | ||||
| [4,41,1] |
Cyclic graph honeycombs
[edit]| Family | |||||
|---|---|---|---|---|---|
| [(3,3,3,3)] |
 |
 |
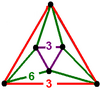 |
 | |
| [(4,3,4,3)] |
 |
 |
 |
 |
 |
| [(5,3,5,3)] |
 |
 |
 |
 |
 |
| [(6,3,6,3)] |
| Family | ||||
|---|---|---|---|---|
| [(4,3,3,3)] |
 |
 |
 |
 |
| [(5,3,3,3)] |
 |
 |
 |
 |
| [(6,3,3,3)] |
||||
| [(5,3,4,3)] |
 |
 |
 |
 |
| [(6,3,5,3)] |
| Family | ||||||||
|---|---|---|---|---|---|---|---|---|
| [(4,4,4,3)] |
||||||||
| [(4,4,4,4)] |
