User:Tomruen/nonsimplex domain honeycombs
Appearance
 Full domain |
 Half domain |
Example compact hyperbolic honeycombs in nonsimplectic domain, a trigonal trapezohedron, with a hexagonal coxeter diagram. the domain is constructed from an index 6 subgroup of [(4,3,4,3)] as [(4,3,4,3*)]:






 ↔
↔ 


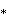 ↔
↔ 





If two pairs of mirrors have the same ring state, they can be mapped into an extended symmetry with a half domain:






 ↔
↔ 





[(4,3,4,3)]
[edit]| Name | Honeycomb | Cells | Subgroup tiling |
Vertex figure |
Perspective | ||
|---|---|---|---|---|---|---|---|
| Symmetry template | ↔ |
||||||
| Cubic-octahedral | ↔ ↔ |

|

|

| |||
| Cyclotruncated octahedral-cubic |
↔ ↔ |

|

|

| |||
Trigonal trapezohedron
[edit]| Honeycomb | Extended symmetry |
Cells | Subgroup tilings | Vertex figure | |||||
|---|---|---|---|---|---|---|---|---|---|
| 4.4.4 | 4.6.6 | 3.4.3.4 | 3.3.3.3 | 3.6.6 | 3.3.3 | ||||
↔ |
[ ] |
 
| |||||||
↔ |
 
| ||||||||
↔ |
(2) |
(6) |
(1) |
(2) |
 
|

| |||
↔ |
[2]+ |
 
| |||||||
↔ ↔ |
[3] |
(8) |
(12) |
(6) |

|

| |||
↔ ↔ |
[6,2+] |
(2) |
(6) |

|
| ||||
*3232 tilings
[edit]


 ↔
↔ 



| Coxeter diagram | ||||
|---|---|---|---|---|
| Vertex figure | 66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 |
| Image | 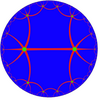
|

|

|

|
| Dual | 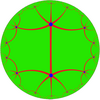
|

|
Half trigonal trapezohedron
[edit]





| # | Honeycomb | Cells | Subgroup tiling |
Vertex figure |
Perspective | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | = |

|

| |||||||
| 4 | - | |||||||||
| 5 | ||||||||||
| 6 | - | |||||||||
| 7 | - | |||||||||
| 8 | - | - | ||||||||
| 9 | = |
- | 
|
|||||||
| 10 | = |
- | ||||||||
| 11 | = |
- | - | - | ||||||
| 12 | = |
- | 
|

| ||||||
